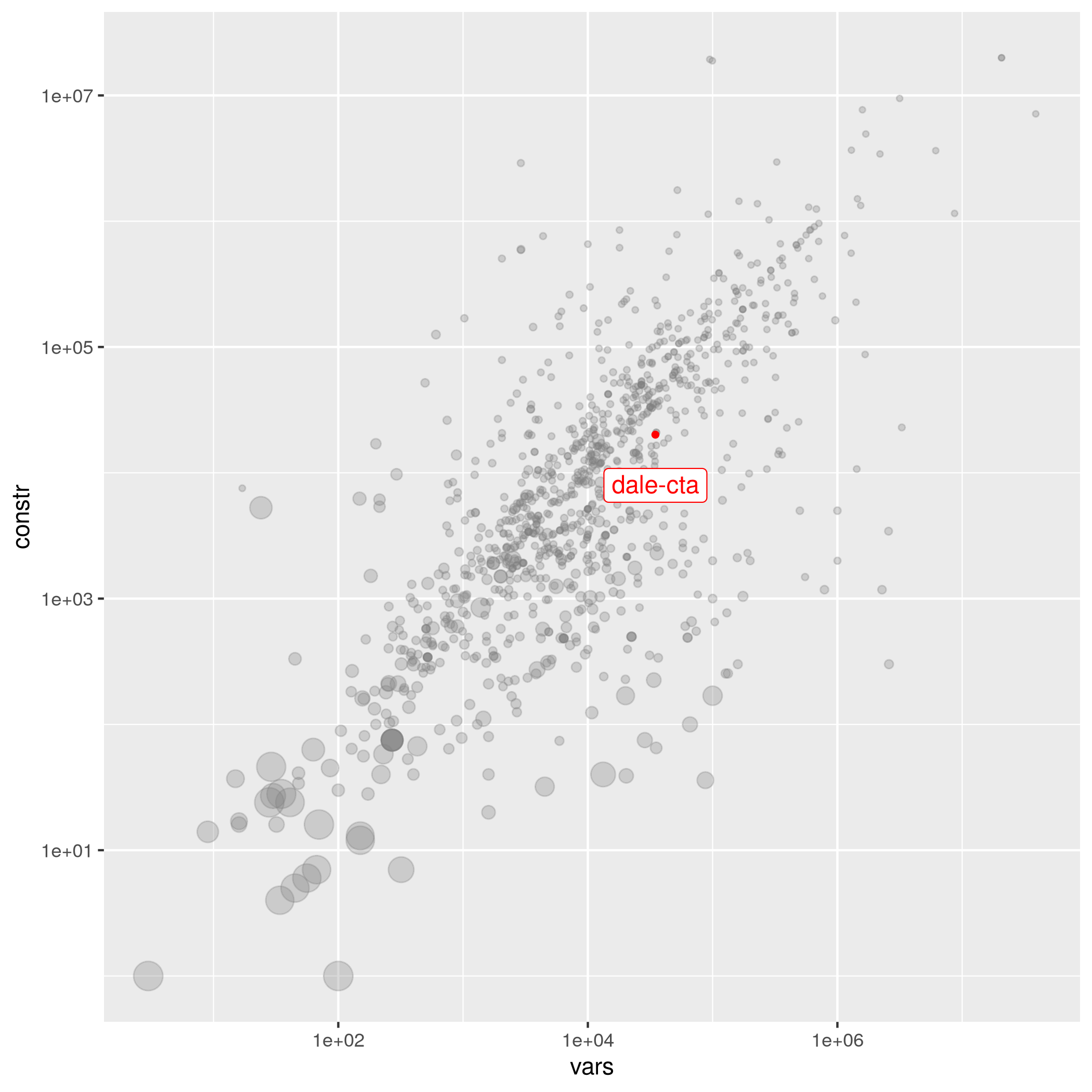
dale-cta

decomposition numerics variable_bound mixed_binary

Submitter	Variables	Constraints	Density	Status	Group	Objective	MPS File
Jordi Castro	37951	20097	1.38245e-04	easy	cta	0	dale-cta.mps.gz

Set of MILP instances of the CTA (Controlled Tabular Adjustment) problem, a method to protect statistical tabular data, belonging to the field of SDC (Statistical Disclosure Control). Raw data of instances are real or pseudo-real, provided by several National Statistical Agencies. We generated the CTA problem for these data.

Location of instance in collection

Instance Statistics

Detailed explanation of the following tables can be found here.

Size Related Properties
	Original	Presolved
Variables	37951	34785
Constraints	20097	20097
Binaries	4923	4923
Integers	0	0
Continuous	33028	29862
Implicit Integers	0	0
Fixed Variables	3166	0
Nonzero Density	0.000138245	0.000141770
Nonzeroes	105440	99108

Constraint Classification Properties
	Original	Presolved
Total	20097	20097
Empty	0	0
Free	0	0
Singleton	0	0
Aggregations	0	0
Precedence	0	0
Variable Bound	19692	19692
Set Partitioning	0	0
Set Packing	0	0
Set Covering	0	0
Cardinality	0	0
Invariant Knapsack	0	0
Equation Knapsack	0	0
Bin Packing	0	0
Knapsack	0	0
Integer Knapsack	0	0
Mixed Binary	405	405
General Linear	0	0
Indicator	0	0

Structure

Available nonzero structure and decomposition information. Further information can be found here.

Nonzero entries of original problem

Nonzero entries after trivial presolving

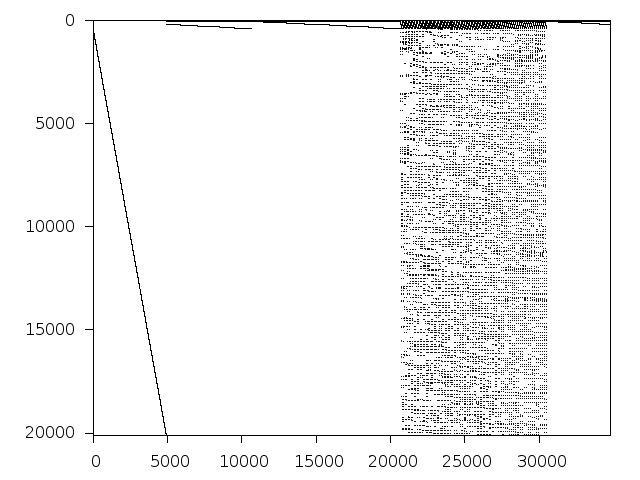
Decomposed structure of original problem (dec-file)

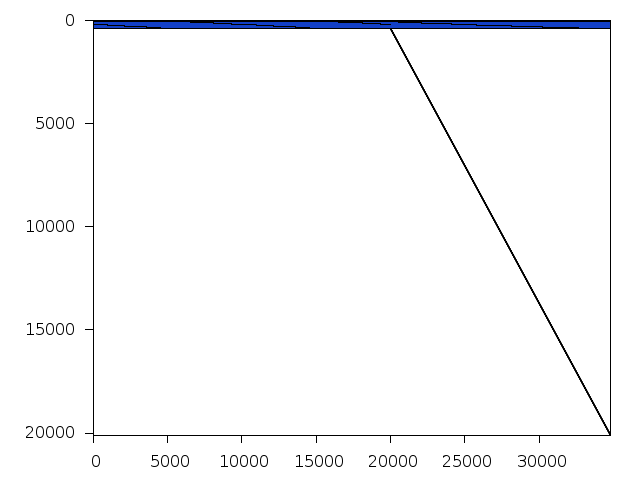
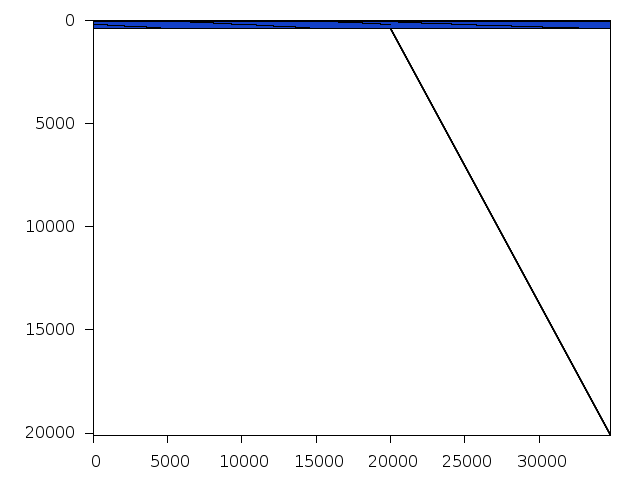
Decomposed structure after trivial presolving (dec-file)

	value	min	median	mean	max
Components	3.692318
Constraint %		0.0199035	0.0199035	0.0199035	0.0199035
Variable %		0.0086200	0.0086200	0.0086200	0.0086200
Score	0.979763

Best Known Solution(s)

No solution available for dale-cta .

Similar instances in collection

The following instances are most similar to dale-cta in the collection. This similarity analysis is based on 100 scaled instance features describing properties of the variables, objective function, bounds, constraints, and right hand sides.

Instance	Status	Variables	Binaries	Continuous	Constraints	Nonz.	Submitter	Group	Objective	Tags
tr12-30	easy	1080	360	720	750	2508	MIPLIB submission pool	–	130595.9999999999	benchmark decomposition benchmark_suitable aggregations variable_bound mixed_binary
bg512142	hard	792	240	552	1307	3953	A. Miller	–	184202.75	aggregations precedence variable_bound mixed_binary
dg012142	hard	2080	640	1440	6310	14795	A. Miller	–	2300867	aggregations precedence variable_bound mixed_binary
mc11	easy	3040	1520	1520	1920	6080	F. Ortega, L. Wolsey	mc	11688.99999999966	benchmark decomposition benchmark_suitable variable_bound mixed_binary
mc8	easy	3040	1520	1520	1920	6080	F. Ortega, L. Wolsey	mc	1566	decomposition benchmark_suitable variable_bound mixed_binary

Reference

@ARTICLE{Castro2006,
  author =       {J. Castro},
  title =        {Minimum-distance controlled perturbation methods for large-scale tabular data protection},
  journal =      {European Journal of Operational Research},
  year =         {2006},
  volume =       {171},
  pages =        {39--52},
}
@ARTICLE{Castro2011,
  author =       {J. A. González, J. Castro},
  title =        {A heuristic block coordinate descent approach for controlled tabular adjustment},
  journal =      {Computers & Operations Research},
  year =         {2011},
  volume =       {38},
  pages =        {1826--1835},
}
@ARTICLE{Castro2012,
  author =       {J. Castro},
  title =        {Recent advances in optimization techniques for statistical tabular data protection},
  journal =      {European Journal of Operational Research},
  year =         {2012},
  volume =       {216},
  pages =        {257--269},
}

@ARTICLE{CastroFrangioniGentile2014,
  author =       {J. Castro, A. Frangioni, C. Gentile},
  title =        {Perspective reformulations of the CTA problem with L2 distances},
  journal =      {Operations Research},
  year =         {2014},
  volume =       {62},
  pages =        {891--909},
}

@ARTICLE{BaenaCastroGonzalez2015,
  author =       {D. Baena, J. Castro, J. A. González},
  title =        {Fix-and-relax approaches for controlled tabular adjustment},
  journal =      {Computers & Operations Research},
  year =         {2015},
  volume =       {58},
  pages =        {41--52},
}