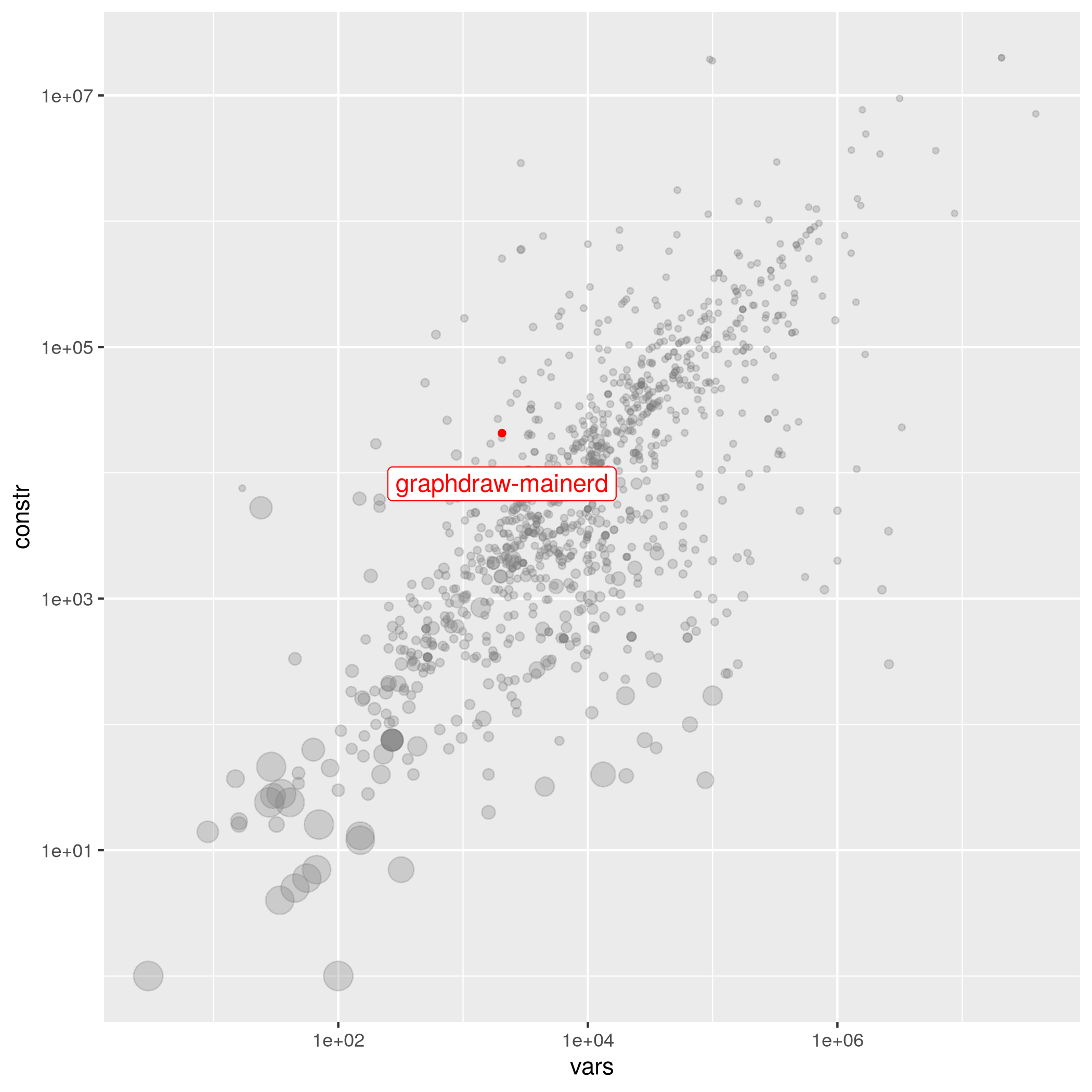
graphdraw-mainerd

variable_bound set_partitioning invariant_knapsack mixed_binary general_linear

Submitter	Variables	Constraints	Density	Status	Group	Objective	MPS File
Cézar Augusto Nascimento e Silva	2050	20661	1.47208e-03	open	graphdraw	38841.9999999991*	graphdraw-mainerd.mps.gz

In the Graph Drawing problem a set of symbols must be placed in a plane and their connections routed. The objective is to produce aesthetically pleasant, easy to read diagrams. As a primary concern one usually tries to minimize edges crossing, edges’ length, waste of space and number of bents in the connections. When formulated with these constraints the problem becomes NP-Hard . In practice many additional complicating requirements can be included, such as non-uniform sizes for symbols. Thus, some heuristics such as the generalized force-direct method and Simulated Annealing have been proposed to tackle this problem. uses a grid structure to approach the Entity-Relationship (ER) drawing problem, emphasizing the differences between ER drawing and the more classical circuit drawing problems. presented different ways of producing graph layouts (e.g.: tree, orthogonal, visibility representations, hierarchic, among others) for general graphs with applications on different subjects. The ability to automatically produce high quality layouts is very important in many applications, one of these is Software Engineering: the availability of easy to understand ER diagrams, for instance, can improve the time needed for developers to master database models and increase their productivity. Our solution approach involves two phases: (\(i\)) firstly the optimal placement of entities is solved, i.e.: entities are positioned so as to minimize the distances between connected entities; and (\(ii\)) secondly, edges are routed minimizing bends and avoiding the inclusion of connectors too close. We present the model for the first phase of our problem.

Location of instance in collection

Instance Statistics

Detailed explanation of the following tables can be found here.

Size Related Properties
	Original	Presolved
Variables	2050	2050
Constraints	20661	20661
Binaries	1860	1860
Integers	62	62
Continuous	128	128
Implicit Integers	0	0
Fixed Variables	0	0
Nonzero Density	0.00147208	0.00147208
Nonzeroes	62350	62350

Constraint Classification Properties
	Original	Presolved
Total	20661	20661
Empty	0	0
Free	0	0
Singleton	0	0
Aggregations	0	0
Precedence	0	0
Variable Bound	157	157
Set Partitioning	465	465
Set Packing	0	0
Set Covering	0	0
Cardinality	0	0
Invariant Knapsack	17980	17980
Equation Knapsack	0	0
Bin Packing	0	0
Knapsack	0	0
Integer Knapsack	0	0
Mixed Binary	67	67
General Linear	1992	1992
Indicator	0	0

Structure

Available nonzero structure and decomposition information. Further information can be found here.

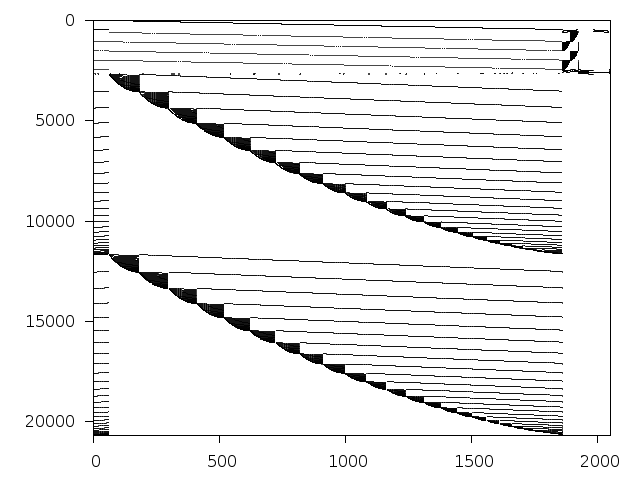
Nonzero entries of original problem

Nonzero entries after trivial presolving

Decomposed structure of original problem (dec-file)

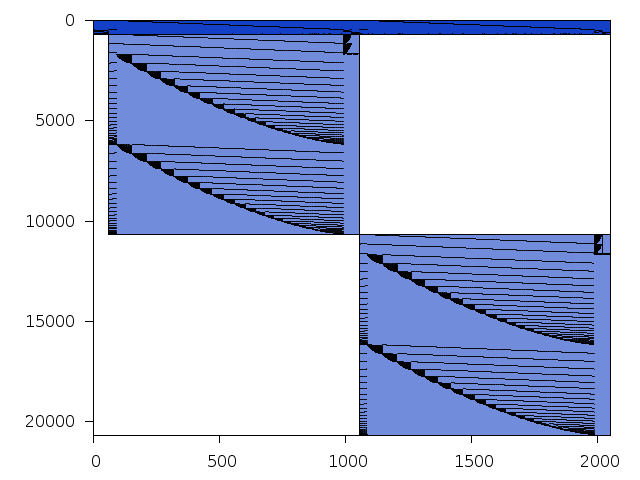
Decomposed structure after trivial presolving (dec-file)

	value	min	median	mean	max
Components	0.4771212
Constraint %		48.3326	48.3326	48.3326	48.3326
Variable %		48.4878	48.4878	48.4878	48.4878
Score	0.4979440

Best Known Solution(s)

Find solutions below. Download the archive containing all solutions from the Download page.

## Warning in lapply(df["exactobjval"], as.numeric): NAs introduced by coercion

ID	Objective	Cons. Viol	Submitter	Date	Description
6	38842	0e+00	Mars Davletshin	2024-07-12	Obtained by OptVerse solver
5	38849	0e+00	Dongdong Wan	2024-07-01	Taylor Solver - Taylor Lab of Huawei Solver
4	39853	0e+00	Edward Rothberg	2020-04-22	Obtained with Gurobi 9.0 using the solution improvement heuristic
3	44372	0e+00	Frederic Didier	2020-01-22	Obtained with Google OR-tools using 8 Threads through generating subproblems by fixing part of the current solution and trying to solve them with a sub CP-SAT solver
2	49016	0e+00	Robert Ashford and Alkis Vazacopoulus	2019-12-18	Found using ODH\|CPlex
1	49949	3e-07	-	2018-10-13	Solution found during MIPLIB2017 problem selection.

Similar instances in collection

The following instances are most similar to graphdraw-mainerd in the collection. This similarity analysis is based on 100 scaled instance features describing properties of the variables, objective function, bounds, constraints, and right hand sides.

Instance	Status	Variables	Binaries	Integers	Continuous	Constraints	Nonz.	Submitter	Group	Objective	Tags
graphdraw-opmanager	open	4812	4512	96	204	75395	227160	Cézar Augusto Nascimento e Silva	graphdraw	99455.49999999904*	variable_bound set_partitioning invariant_knapsack mixed_binary general_linear
graphdraw-grafo2	open	9258	8844	134	280	203455	612366	Cézar Augusto Nascimento e Silva	graphdraw	68613.49999999868*	variable_bound set_partitioning invariant_knapsack mixed_binary general_linear
graphdraw-domain	easy	254	180	20	54	865	2600	Cézar Augusto Nascimento e Silva	graphdraw	19685.99997550038	benchmark benchmark_suitable variable_bound set_partitioning invariant_knapsack mixed_binary general_linear
graphdraw-gemcutter	easy	166	112	16	38	474	1420	Cézar Augusto Nascimento e Silva	graphdraw	7118.5	benchmark_suitable variable_bound set_partitioning invariant_knapsack mixed_binary general_linear
neos-3402294-bobin	easy	2904	2616	0	288	591076	2034888	Jeff Linderoth	neos-pseudoapplication-71	0.06724999999999949	benchmark benchmark_suitable precedence set_partitioning set_covering invariant_knapsack mixed_binary

Reference

@article{ESILVA2017207,
title = {Drawing graphs with mathematical programming and variable neighborhood search},
journal = {Electronic Notes in Discrete Mathematics},
volume = {58},
pages = {207--214},
year = {2017},
issn = {1571-0653},
doi = {http://dx.doi.org/10.1016/j.endm.2017.03.027},
author = {Cézar Augusto N. e Silva and Haroldo Gambini Santos}
}