gus-sch

decomposition aggregations precedence variable_bound set_packing set_covering cardinality invariant_knapsack integer_knapsack mixed_binary general_linear

Submitter	Variables	Constraints	Density	Status	Group	Objective	MPS File
Alexandra M. Newman	5475	5984	1.01137e-03	easy	–	-1167	gus-sch.mps.gz

course scheduling model

Location of instance in collection

Instance Statistics

Detailed explanation of the following tables can be found here.

Size Related Properties
	Original	Presolved
Variables	5475	2258
Constraints	5984	2585
Binaries	2736	1924
Integers	2736	331
Continuous	3	3
Implicit Integers	0	0
Fixed Variables	0	0
Nonzero Density	0.00101137	0.00232417
Nonzeroes	33135	13566

Constraint Classification Properties
	Original	Presolved
Total	5998	2610
Empty	0	0
Free	0	0
Singleton	35	0
Aggregations	48	46
Precedence	0	1596
Variable Bound	5473	657
Set Partitioning	0	0
Set Packing	0	37
Set Covering	0	47
Cardinality	2	2
Invariant Knapsack	48	41
Equation Knapsack	0	0
Bin Packing	0	0
Knapsack	0	0
Integer Knapsack	120	89
Mixed Binary	116	2
General Linear	156	93
Indicator	0	0

Structure

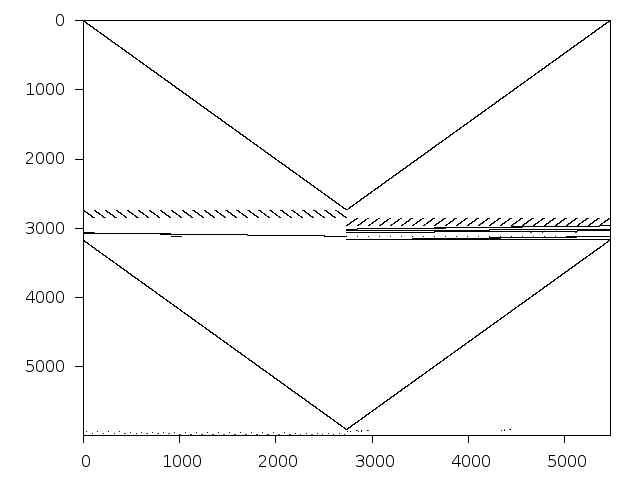
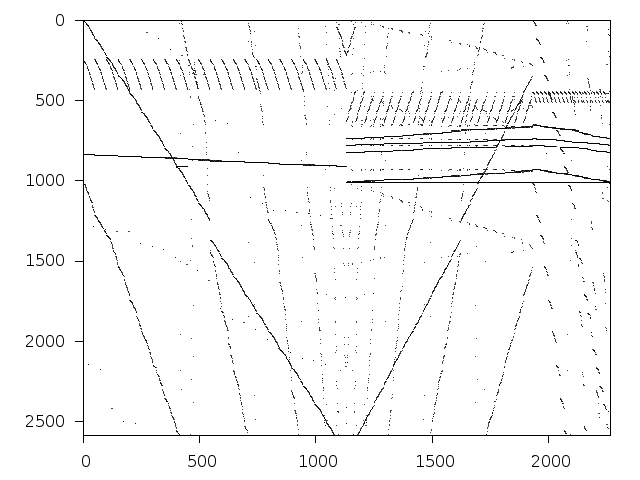
Available nonzero structure and decomposition information. Further information can be found here.

Nonzero entries of original problem

Nonzero entries after trivial presolving

Decomposed structure of original problem (dec-file)

Decomposed structure after trivial presolving (dec-file)

	value	min	median	mean	max
Components	3.033826
Constraint %		0.0771307	0.0821657	0.0771307	0.192827
Variable %		0.0883002	0.0921838	0.0883002	0.176600
Score	0.889957

Best Known Solution(s)

Find solutions below. Download the archive containing all solutions from the Download page.

ID	Objective	Exact	Int. Viol	Cons. Viol	Obj. Viol	Submitter	Date	Description
1	-1167	-1167	0	0	0	-	2018-10-12	Solution found during MIPLIB2017 problem selection.

Similar instances in collection

The following instances are most similar to gus-sch in the collection. This similarity analysis is based on 100 scaled instance features describing properties of the variables, objective function, bounds, constraints, and right hand sides.

Instance	Status	Variables	Binaries	Integers	Continuous	Constraints	Nonz.	Submitter	Group	Objective	Tags
comp08-2idx	easy	11554	11487	67	0	12536	51608	Matias Sørensen	coursetimetabling	37	decomposition benchmark_suitable precedence variable_bound set_packing cardinality invariant_knapsack mixed_binary general_linear
mkc	hard	5325	5323	0	2	3411	17038	J. Kalagnanam, M. Dawande	–	-563.8460100132	decomposition precedence variable_bound set_packing invariant_knapsack binpacking mixed_binary
qiu	easy	840	48	0	792	1192	3432	Y. Chiu, J. Eckstein	–	-132.87313695	benchmark_suitable precedence variable_bound mixed_binary
sct5	open	37265	23004	0	14261	13304	147037	Siemens	sct	-228.119492755556*	decomposition aggregations precedence invariant_knapsack knapsack mixed_binary general_linear
neos-555343	easy	3815	3800	15	0	3326	16967	NEOS Server Submission	neos-pseudoapplication-15	1512800	decomposition benchmark_suitable aggregations precedence invariant_knapsack equation_knapsack binpacking mixed_binary general_linear

Reference

I don't know too much about this one.