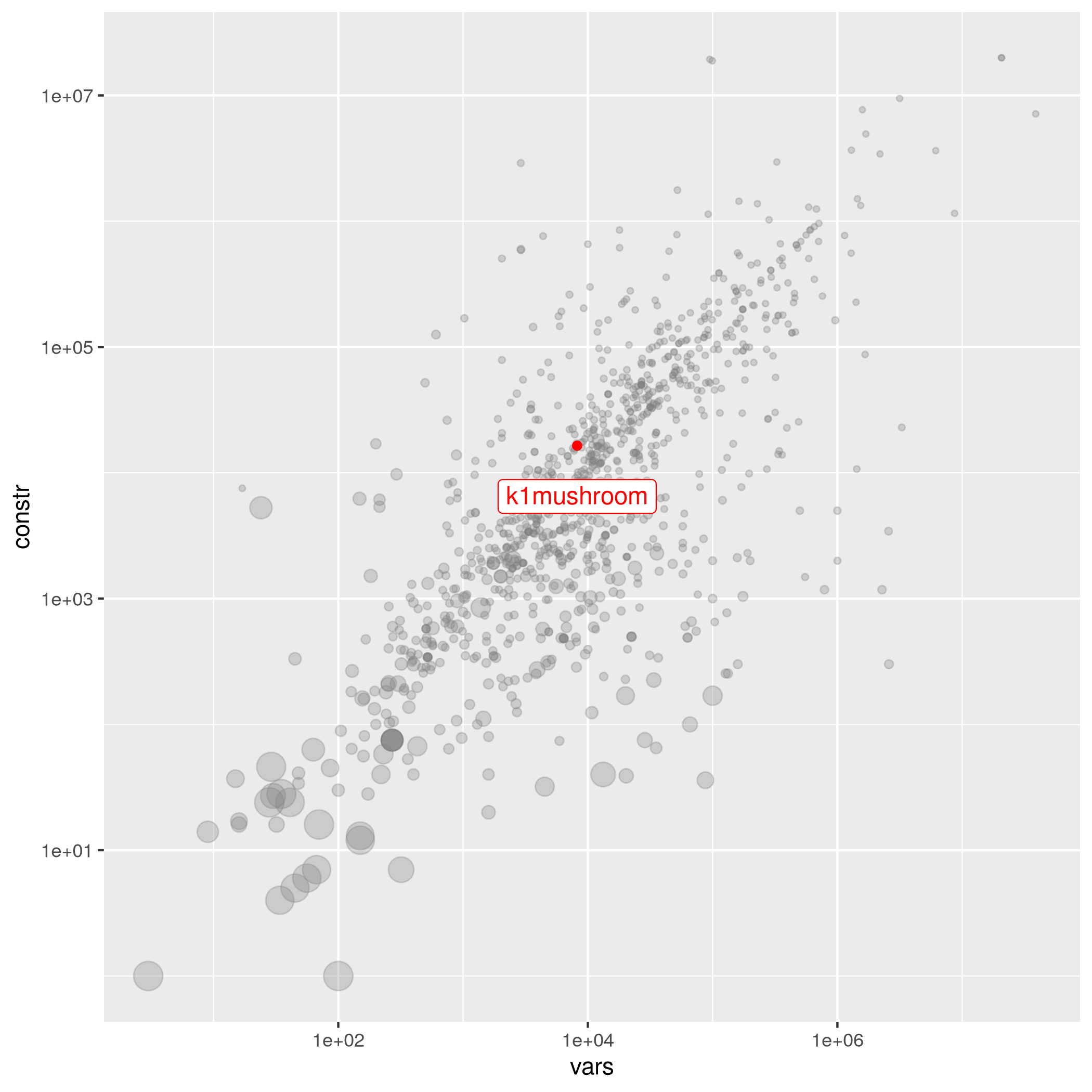
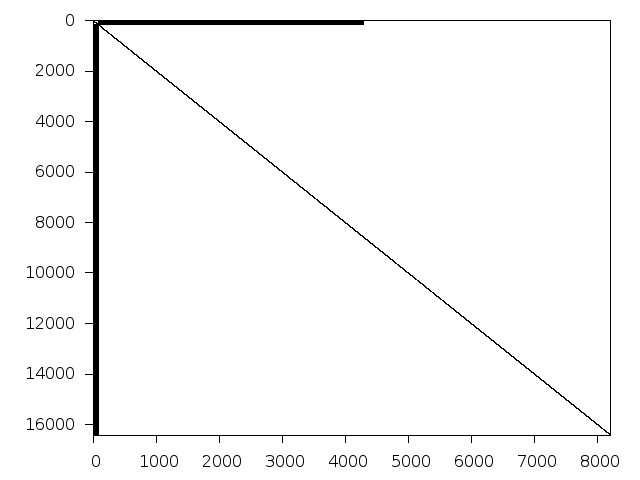
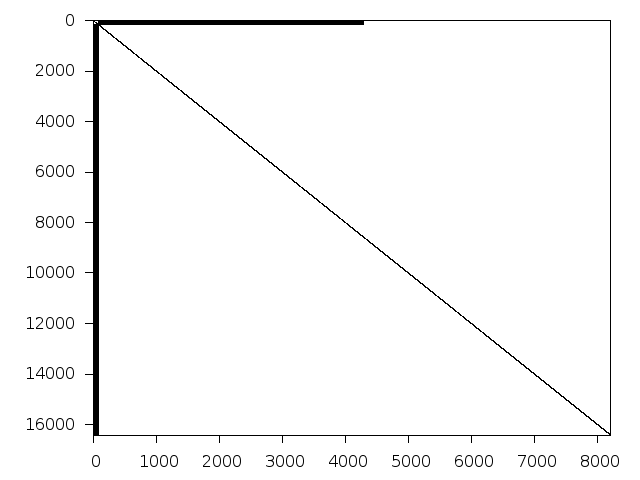
k1mushroom

benchmark benchmark_suitable set_covering binpacking general_linear

Submitter	Variables	Constraints	Density	Status	Group	Objective	MPS File
Gleb Belov	8211	16419	1.25945e-02	easy	k1mushroom	-3288	k1mushroom.mps.gz

Linearized Constraint Programming models of the MiniZinc Challenges 2012-2016. I should be able to produce versions with indicator constraints supported by Gurobi and CPLEX, however don’t know if you can use them and if there is a standard format. These MPS were produced by Gurobi 7.0.2 using the MiniZinc develop branch on eb536656062ca13325a96b5d0881742c7d0e3c38

Location of instance in collection

Instance Statistics

Detailed explanation of the following tables can be found here.

Size Related Properties
	Original	Presolved
Variables	8211	8210
Constraints	16419	16419
Binaries	8210	8209
Integers	1	1
Continuous	0	0
Implicit Integers	0	0
Fixed Variables	1	0
Nonzero Density	0.0125945	0.0125960
Nonzeroes	1697950	1697950

Constraint Classification Properties
	Original	Presolved
Total	16419	16419
Empty	0	0
Free	0	0
Singleton	0	0
Aggregations	0	0
Precedence	0	0
Variable Bound	0	0
Set Partitioning	0	0
Set Packing	0	0
Set Covering	0	8209
Cardinality	0	0
Invariant Knapsack	86	0
Equation Knapsack	0	0
Bin Packing	8209	8209
Knapsack	8123	0
Integer Knapsack	0	0
Mixed Binary	0	0
General Linear	1	1
Indicator	0	0

Structure

Available nonzero structure and decomposition information. Further information can be found here.

Nonzero entries of original problem

Nonzero entries after trivial presolving

Decomposed structure of original problem (dec-file)

Decomposed structure after trivial presolving (dec-file)

	value	min	median	mean	max
Components	0.301030
Constraint %		99.9939	99.9939	99.9939	99.9939
Variable %		99.9756	99.9756	99.9756	99.9756
Score	0.000244

Best Known Solution(s)

Find solutions below. Download the archive containing all solutions from the Download page.

ID	Objective	Exact	Int. Viol	Cons. Viol	Obj. Viol	Submitter	Date	Description
1	-3288	-3288	0	0	0	-	2018-10-12	Solution found during MIPLIB2017 problem selection.

Similar instances in collection

The following instances are most similar to k1mushroom in the collection. This similarity analysis is based on 100 scaled instance features describing properties of the variables, objective function, bounds, constraints, and right hand sides.

Instance	Status	Variables	Binaries	Integers	Continuous	Constraints	Nonz.	Submitter	Group	Objective	Tags
splice1k1	easy	3253	3252	1	0	6505	1761016	Gleb Belov	splice	-394	benchmark benchmark_suitable set_covering binpacking general_linear
hypothyroid-k1	easy	2602	2601	1	0	5195	433884	Gleb Belov	hypothyroid	-2851	benchmark benchmark_suitable aggregations precedence set_covering binpacking general_linear
usafa	open	228648	216357	12291	0	1377561	16485102	Christopher Daniel Richards	–	160.1671357657*	aggregations precedence variable_bound set_partitioning set_packing invariant_knapsack binpacking integer_knapsack general_linear
neos-2991472-kalu	open	12105	12096	0	9	18170	13709358	Jeff Linderoth	neos-pseudoapplication-77	12*	set_packing set_covering invariant_knapsack binpacking knapsack mixed_binary
neos8	easy	23228	23224	4	0	46324	313180	NEOS Server Submission	neos-pseudoapplication-15	-3719	benchmark benchmark_suitable precedence set_packing cardinality invariant_knapsack binpacking general_linear

Reference

@Inbook{Belov2016,
author="Belov, Gleb
and Stuckey, Peter J.
and Tack, Guido
and Wallace, Mark",
editor="Rueher, Michel",
title="Improved Linearization of Constraint Programming Models",
bookTitle="Principles and Practice of Constraint Programming: 22nd International Conference, CP 2016, Toulouse, France, September 5-9, 2016, Proceedings",
year="2016",
publisher="Springer International Publishing",
pages="49--65",
isbn="978-3-319-44953-1",
doi="10.1007/978-3-319-44953-1_4",
url="http://dx.doi.org/10.1007/978-3-319-44953-1_4"
}