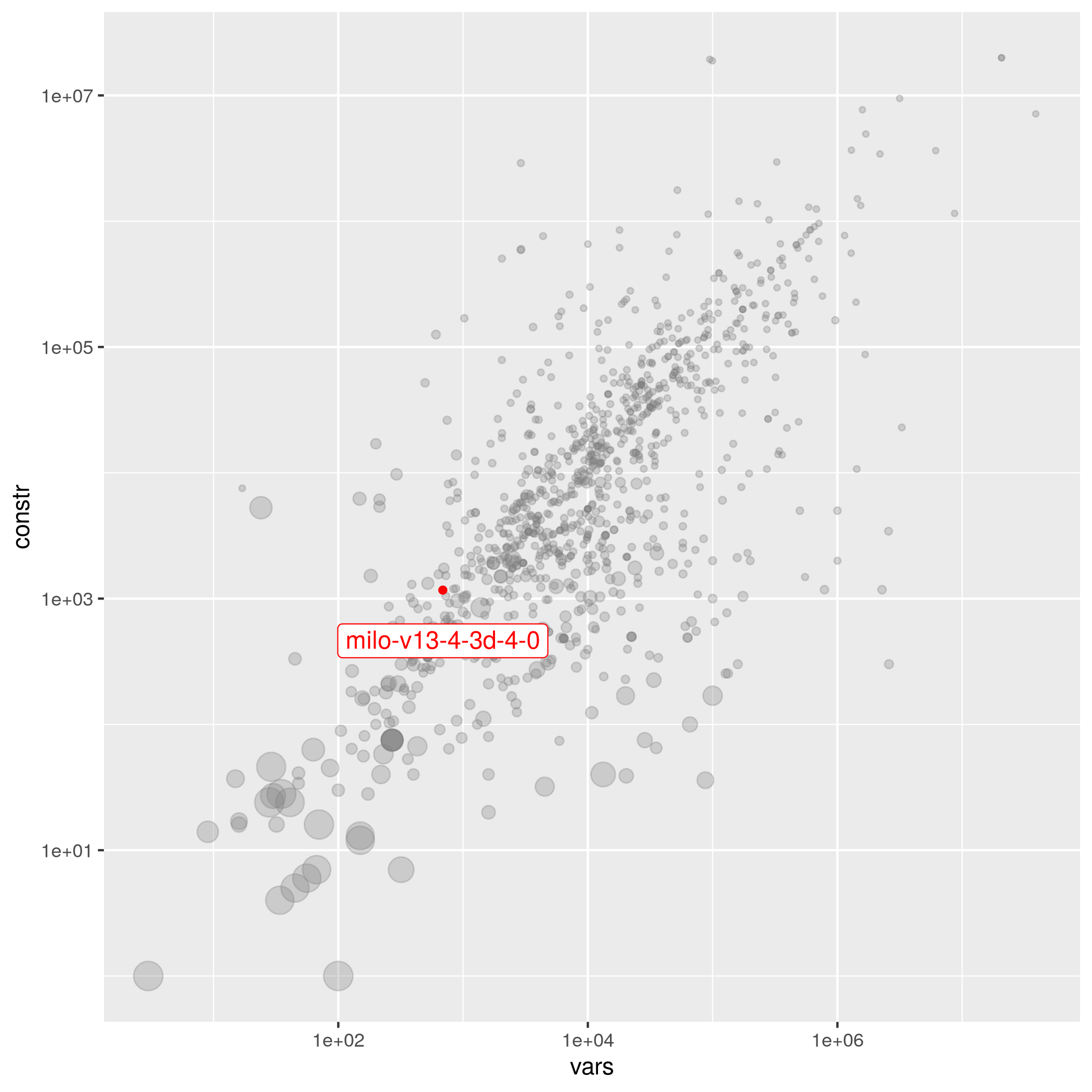
milo-v13-4-3d-4-0

aggregations variable_bound mixed_binary general_linear

Submitter	Variables	Constraints	Density	Status	Group	Objective	MPS File
Tamas Terlaky	688	1328	3.60308e-03	open	milo	358152.2621937089*	milo-v13-4-3d-4-0.mps.gz

The models come from structural design optimization where the objective is to minimize the total weight of 2 and 3 dimensional cantilevers. The 2D examples are simpler, and GuRobi can solve the 40_1 and 58_1 instances, while struggles with 75_1. The 3D examples are more challenging. The x_0 and x_1 models are two different modeling of the same identical problems, so their optimal value is the same. The 1_x and 2_x problems are solved by GuRoBi, the 3_x and 4_x are not solved in reasonable time.

Location of instance in collection

Instance Statistics

Detailed explanation of the following tables can be found here.

Size Related Properties
	Original	Presolved
Variables	688	688
Constraints	1328	1168
Binaries	160	160
Integers	0	80
Continuous	528	448
Implicit Integers	0	80
Fixed Variables	0	0
Nonzero Density	0.00360308	0.00389754
Nonzeroes	3292	3132

Constraint Classification Properties
	Original	Presolved
Total	1328	1168
Empty	0	0
Free	0	0
Singleton	160	0
Aggregations	164	164
Precedence	0	0
Variable Bound	400	400
Set Partitioning	0	0
Set Packing	0	0
Set Covering	0	0
Cardinality	0	0
Invariant Knapsack	0	0
Equation Knapsack	0	0
Bin Packing	0	0
Knapsack	0	0
Integer Knapsack	0	0
Mixed Binary	604	524
General Linear	0	80
Indicator	0	0

Structure

Available nonzero structure and decomposition information. Further information can be found here.

Nonzero entries of original problem

Nonzero entries after trivial presolving

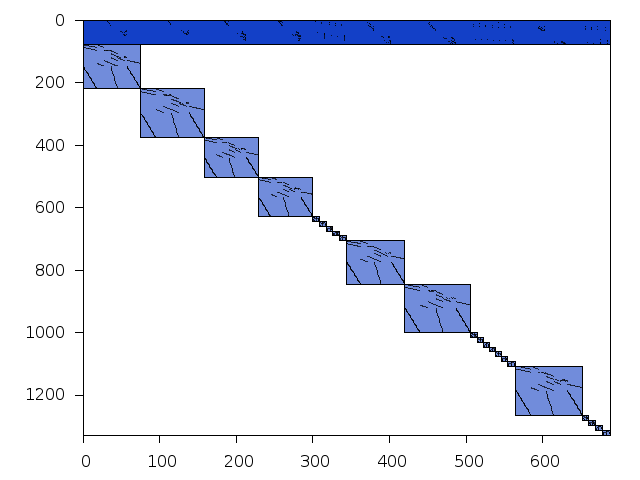
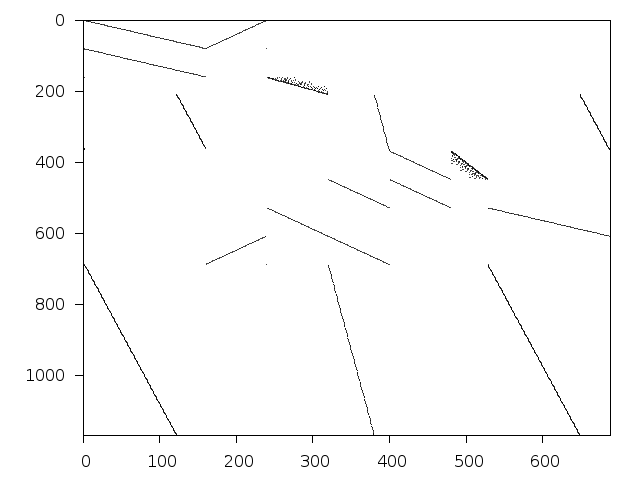
Decomposed structure of original problem (dec-file)

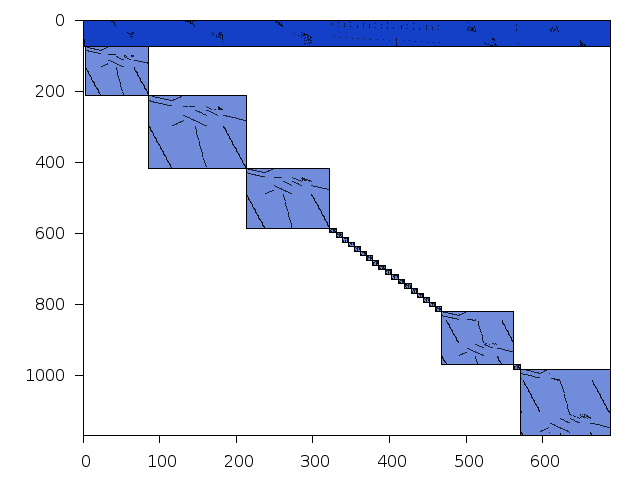
Decomposed structure after trivial presolving (dec-file)

	value	min	median	mean	max
Components	1.653213
Constraint %		1.11301	2.11317	1.11301	44.3493
Variable %		1.16279	2.27273	1.16279	47.3837
Score	0.713683

Best Known Solution(s)

Find solutions below. Download the archive containing all solutions from the Download page.

## Warning in lapply(df["exactobjval"], as.numeric): NAs introduced by coercion

ID	Objective	Exact	Int. Viol	Cons. Viol	Obj. Viol	Submitter	Date	Description
2	358152.3		0	0	0	Robert Ashford and Alkis Vazacopoulus	2019-12-18	Found using ODH\|CPlex
1	363893.0	363893	0	0	0	-	2018-10-12	Solution found during MIPLIB2017 problem selection.

Similar instances in collection

The following instances are most similar to milo-v13-4-3d-4-0 in the collection. This similarity analysis is based on 100 scaled instance features describing properties of the variables, objective function, bounds, constraints, and right hand sides.

Instance	Status	Variables	Binaries	Integers	Continuous	Constraints	Nonz.	Submitter	Group	Objective	Tags
milo-v13-4-3d-3-0	hard	516	120	0	396	996	2456	Tamas Terlaky	milo	273238.08563337	aggregations variable_bound mixed_binary general_linear
milo-v12-6-r1-58-1	hard	4440	1500	0	2940	9540	25068	Tamas Terlaky	milo	634081.4112039516	decomposition aggregations precedence variable_bound mixed_binary general_linear
milo-v12-6-r1-75-1	open	5698	1925	0	3773	12243	32174	Tamas Terlaky	milo	1153756.39820567*	decomposition aggregations precedence variable_bound mixed_binary general_linear
milo-v12-6-r2-40-1	easy	2688	840	0	1848	5628	14604	Tamas Terlaky	milo	326481.14282799	benchmark decomposition benchmark_suitable aggregations precedence variable_bound mixed_binary general_linear
supportcase17	easy	1381	732	235	414	2108	5253	Michael Winkler	–	1329.999999999999	benchmark_suitable aggregations precedence variable_bound set_partitioning mixed_binary general_linear

Reference

No bibliographic information available