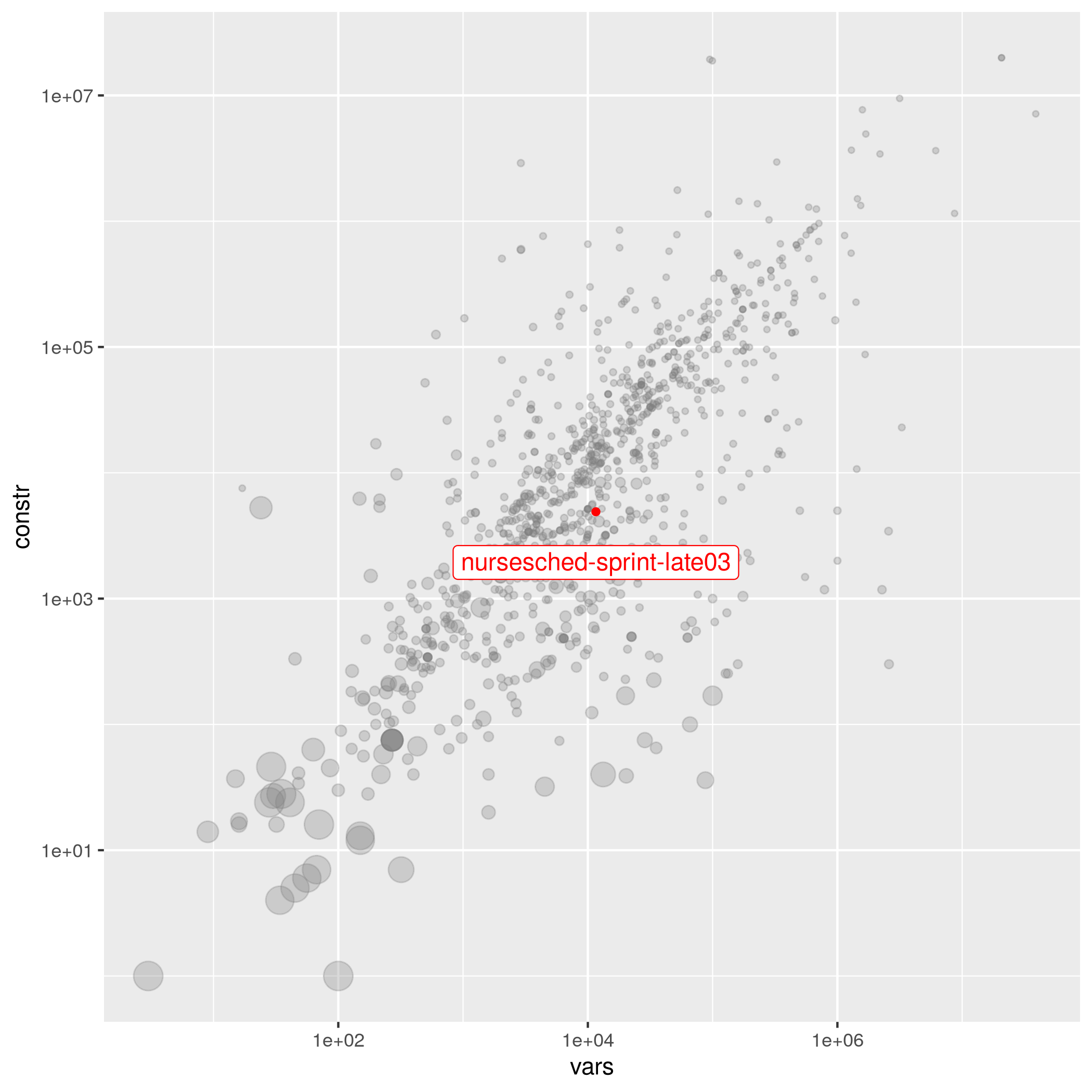
nursesched-sprint-late03

decomposition benchmark_suitable set_partitioning set_packing cardinality invariant_knapsack general_linear

Submitter	Variables	Constraints	Density	Status	Group	Objective	MPS File
Haroldo Gambini Santos	11690	5032	3.54294e-03	easy	nursescheduling	48	nursesched-sprint-late03.mps.gz

Nurse Scheduling Problems from the First International Nurse Rostering Competition - INRC 2010

Location of instance in collection

Instance Statistics

Detailed explanation of the following tables can be found here.

Size Related Properties
	Original	Presolved
Variables	11690	11600
Constraints	5032	4902
Binaries	11670	11580
Integers	20	20
Continuous	0	0
Implicit Integers	0	0
Fixed Variables	0	0
Nonzero Density	0.00354294	0.00366072
Nonzeroes	208410	208160

Constraint Classification Properties
	Original	Presolved
Total	5032	4902
Empty	0	0
Free	0	0
Singleton	10	0
Aggregations	0	0
Precedence	0	0
Variable Bound	120	0
Set Partitioning	632	672
Set Packing	1410	1490
Set Covering	320	0
Cardinality	360	320
Invariant Knapsack	2080	2400
Equation Knapsack	0	0
Bin Packing	0	0
Knapsack	0	0
Integer Knapsack	0	0
Mixed Binary	80	0
General Linear	20	20
Indicator	0	0

Structure

Available nonzero structure and decomposition information. Further information can be found here.

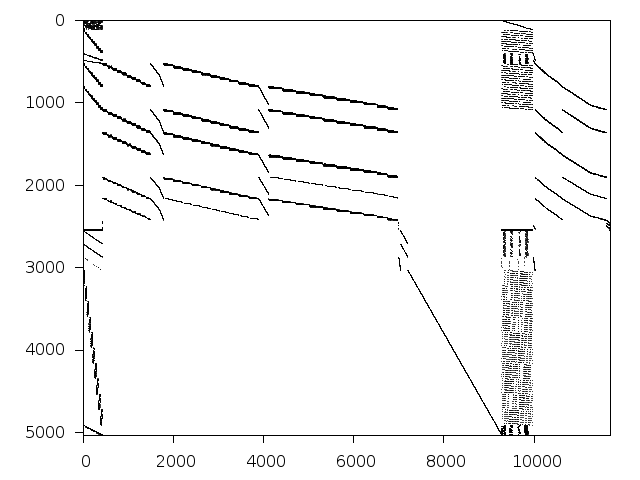
Nonzero entries of original problem

Nonzero entries after trivial presolving

Decomposed structure of original problem (dec-file)

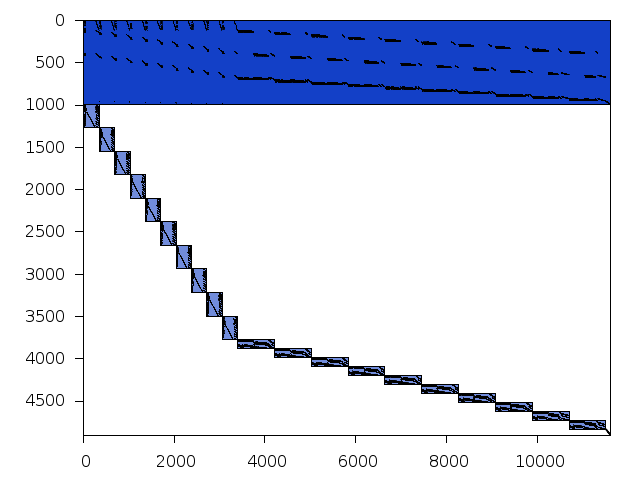
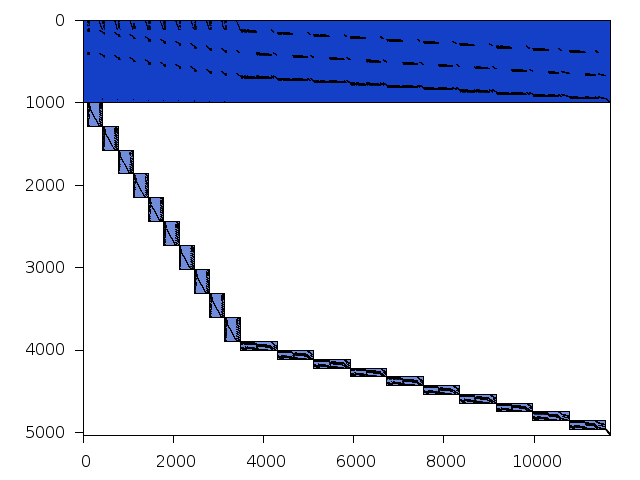
Decomposed structure after trivial presolving (dec-file)

	value	min	median	mean	max
Components	1.491362
Constraint %		0.1427990	2.65878	2.16238	5.67115
Variable %		0.0862069	3.32759	2.91379	6.98276
Score	0.765997

Best Known Solution(s)

Find solutions below. Download the archive containing all solutions from the Download page.

ID	Objective	Exact	Int. Viol	Cons. Viol	Obj. Viol	Submitter	Date	Description
1	48	48	0	0	0	-	2018-10-12	Solution found during MIPLIB2017 problem selection.

Similar instances in collection

The following instances are most similar to nursesched-sprint-late03 in the collection. This similarity analysis is based on 100 scaled instance features describing properties of the variables, objective function, bounds, constraints, and right hand sides.

Instance	Status	Variables	Binaries	Integers	Constraints	Nonz.	Submitter	Group	Objective	Tags
nursesched-medium-hint03	hard	34248	34170	78	14062	622800	Haroldo Gambini Santos	nursescheduling	115	benchmark decomposition benchmark_suitable set_partitioning set_packing cardinality invariant_knapsack general_linear
nursesched-sprint-hidden09	easy	11650	11630	20	4872	208050	Haroldo Gambini Santos	nursescheduling	338	benchmark_suitable set_partitioning set_packing cardinality invariant_knapsack general_linear
nursesched-sprint02	easy	10250	10230	20	3522	204000	Haroldo Gambini Santos	nursescheduling	57.99999999999999	benchmark benchmark_suitable set_partitioning set_packing cardinality invariant_knapsack general_linear
comp12-2idx	open	11863	11820	43	16803	73677	Matias Sørensen	coursetimetabling	291*	decomposition precedence variable_bound set_partitioning cardinality invariant_knapsack mixed_binary general_linear
comp21-2idx	easy	10863	10792	71	14038	57301	Matias Sørensen	coursetimetabling	74	benchmark decomposition benchmark_suitable precedence variable_bound set_partitioning cardinality invariant_knapsack mixed_binary general_linear

Reference

@Article{Santos2016,
author="Santos, Haroldo G.
and Toffolo, T{\'u}lio A. M.
and Gomes, Rafael A. M.
and Ribas, Sabir",
title="Integer programming techniques for the nurse rostering problem",
journal="Annals of Operations Research",
year="2016",
volume="239",
number="1",
pages="225--251",
issn="1572-9338",
doi="10.1007/s10479-014-1594-6",
url="http://dx.doi.org/10.1007/s10479-014-1594-6"
}