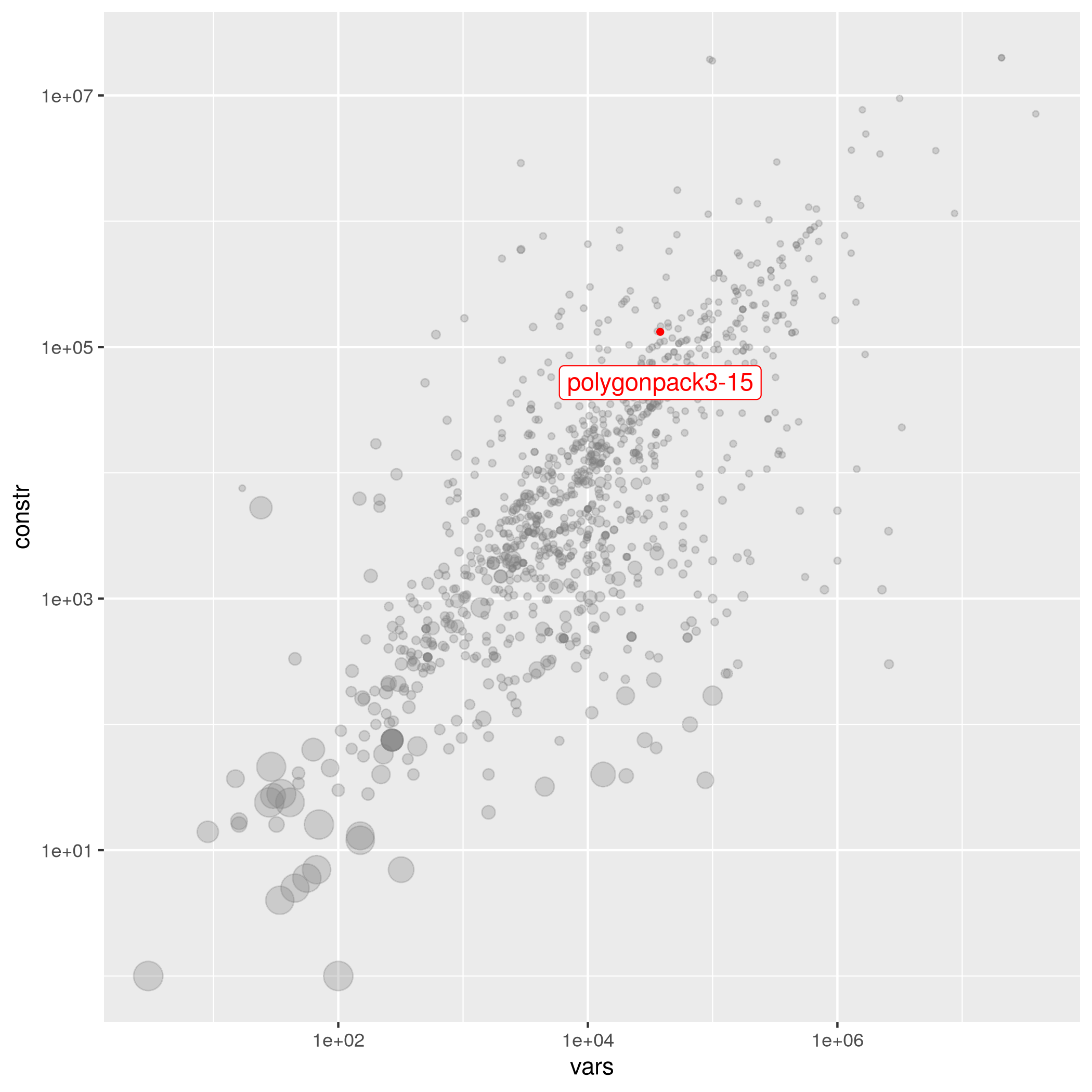
polygonpack3-15
numerics precedence variable_bound set_packing invariant_knapsack mixed_binary
| Submitter | Variables | Constraints | Density | Status | Group | Objective | MPS File |
|---|---|---|---|---|---|---|---|
| Antonio Frangioni | 44237 | 144478 | 1.14523e-04 | open | polygonpack | -55055595.32367724* | polygonpack3-15.mps.gz |
Given a set P of polygons, not necessarily convex, and a rectangle,
we want to find the subset S of P with largest possible total area and a
position every p in S so that there are no overlaps and they are all
included in the rectangle. We allow a small set of rotations (0, 90,
180, 270 degrees) for every polygon. The problem is simplified w.r.t.
the real application because the polygons do not have (fully encircled)
“holes”, which are supposedly filled-in separately, although they can
have “bays”. Models are saved as .lp. Instance LpPackingModel
Instance Statistics
Detailed explanation of the following tables can be found here.
| Original | Presolved | |
|---|---|---|
| Variables | 44237 | 38043 |
| Constraints | 144478 | 131920 |
| Binaries | 44207 | 38013 |
| Integers | 0 | 0 |
| Continuous | 30 | 30 |
| Implicit Integers | 0 | 0 |
| Fixed Variables | 0 | 0 |
| Nonzero Density | 0.000114523 | 0.000131310 |
| Nonzeroes | 731949 | 658997 |
| Original | Presolved | |
|---|---|---|
| Total | 144478 | 131920 |
| Empty | 0 | 0 |
| Free | 0 | 0 |
| Singleton | 0 | 0 |
| Aggregations | 0 | 0 |
| Precedence | 0 | 1239 |
| Variable Bound | 0 | 2 |
| Set Partitioning | 0 | 0 |
| Set Packing | 15 | 13 |
| Set Covering | 0 | 0 |
| Cardinality | 0 | 0 |
| Invariant Knapsack | 1680 | 1460 |
| Equation Knapsack | 0 | 0 |
| Bin Packing | 0 | 0 |
| Knapsack | 0 | 0 |
| Integer Knapsack | 0 | 0 |
| Mixed Binary | 142783 | 129206 |
| General Linear | 0 | 0 |
| Indicator | 0 | 0 |
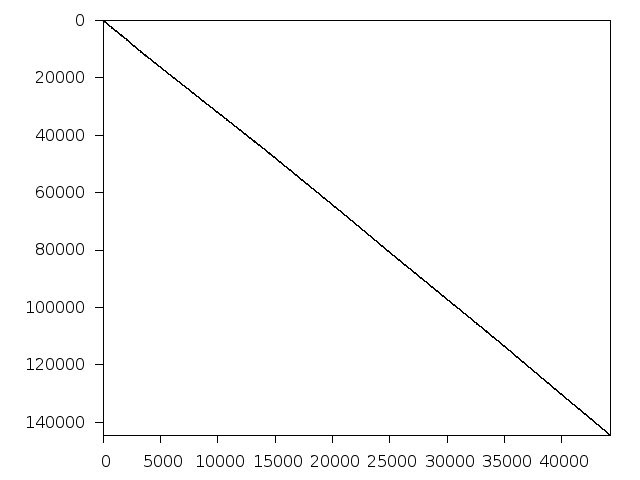
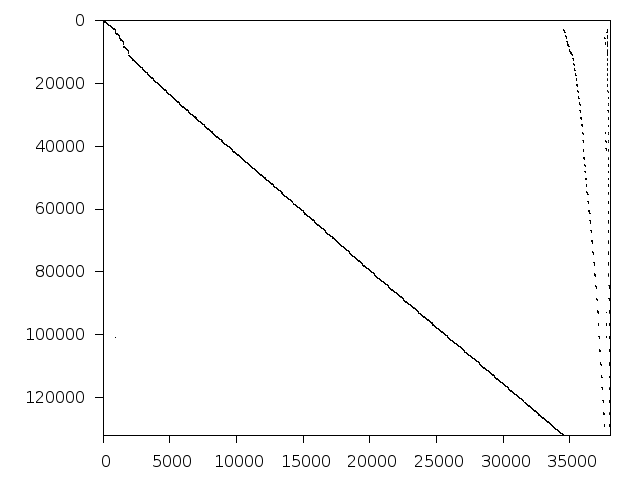
Structure
Available nonzero structure and decomposition information. Further information can be found here.
Decomposed structure of original problem (dec-file)
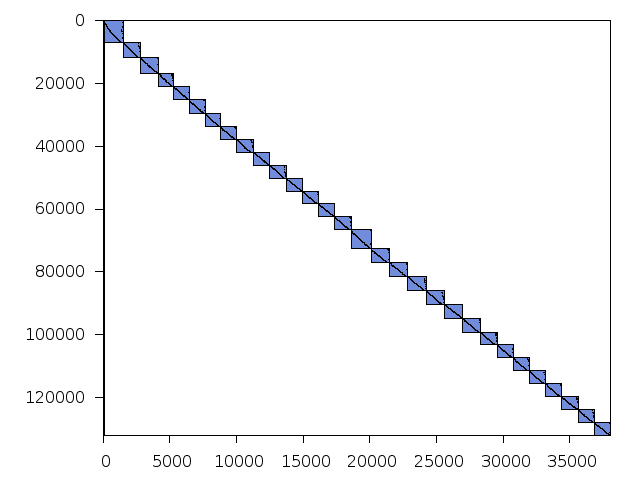
Decomposed structure after trivial presolving (dec-file)
| value | min | median | mean | max | |
|---|---|---|---|---|---|
| Components | 1.255273 | ||||
| Constraint % | 0.000758 | 0.0559162 | 0.0007580 | 0.5086420 | |
| Variable % | 0.005260 | 0.0132976 | 0.0105144 | 0.0394291 | |
| Score | 0.009502 |
Best Known Solution(s)
Find solutions below. Download the archive containing all solutions from the Download page.
## Warning in lapply(df["exactobjval"], as.numeric): NAs introduced by coercion| ID | Objective | Exact | Int. Viol | Cons. Viol | Obj. Viol | Submitter | Date | Description |
|---|---|---|---|---|---|---|---|---|
| 4 | -55055595 | 0 | 0 | 0.0e+00 | Michael Winkler | 2023-11-14 | incumbents found with Gurobi 10.0.2 on AMD EPYC 7313P 16-Core Processor with 264075352 kB memory running with default except for MIPGAP=0 | |
| 3 | -54680307 | 0 | 0 | 0.0e+00 | Edward Rothberg | 2019-12-13 | Obtained with Gurobi 9.0 | |
| 2 | -51149531 | 0 | 0 | 0.0e+00 | Robert Ashford and Alkis Vazacopoulus | 2019-12-18 | Found using ODH|CPlex | |
| 1 | -48143435 | -48143435 | 0 | 0 | 2.6e-06 | - | 2018-10-13 | Solution found during MIPLIB2017 problem selection. |
Similar instances in collection
The following instances are most similar to polygonpack3-15 in the collection. This similarity analysis is based on 100 scaled instance features describing properties of the variables, objective function, bounds, constraints, and right hand sides.
| Instance | Status | Variables | Binaries | Integers | Continuous | Constraints | Nonz. | Submitter | Group | Objective | Tags |
|---|---|---|---|---|---|---|---|---|---|---|---|
| polygonpack5-15 | open | 48163 | 48133 | 0 | 30 | 163429 | 804740 | Antonio Frangioni | polygonpack | -55494653.8357854* | numerics precedence variable_bound set_packing invariant_knapsack mixed_binary |
| polygonpack4-15 | open | 44237 | 44207 | 0 | 30 | 144478 | 731949 | Antonio Frangioni | polygonpack | -63613612.41121812* | numerics set_packing invariant_knapsack mixed_binary |
| polygonpack4-10 | open | 20537 | 20517 | 0 | 20 | 65935 | 339036 | Antonio Frangioni | polygonpack | -53594508.70758325* | numerics set_packing invariant_knapsack mixed_binary |
| polygonpack4-7 | open | 10788 | 10774 | 0 | 14 | 34529 | 178591 | Antonio Frangioni | polygonpack | -51837707.95034043* | numerics set_packing invariant_knapsack mixed_binary |
| rocII-10-11 | open | 22968 | 22616 | 0 | 352 | 52692 | 604216 | Joerg Rambau | rocI | -11.78958471072697* | aggregations precedence variable_bound set_partitioning set_packing mixed_binary |
Reference
No bibliographic information availableLast Update 2024 by Julian Manns
generated with R Markdown
© by Zuse Institute Berlin (ZIB)
Imprint