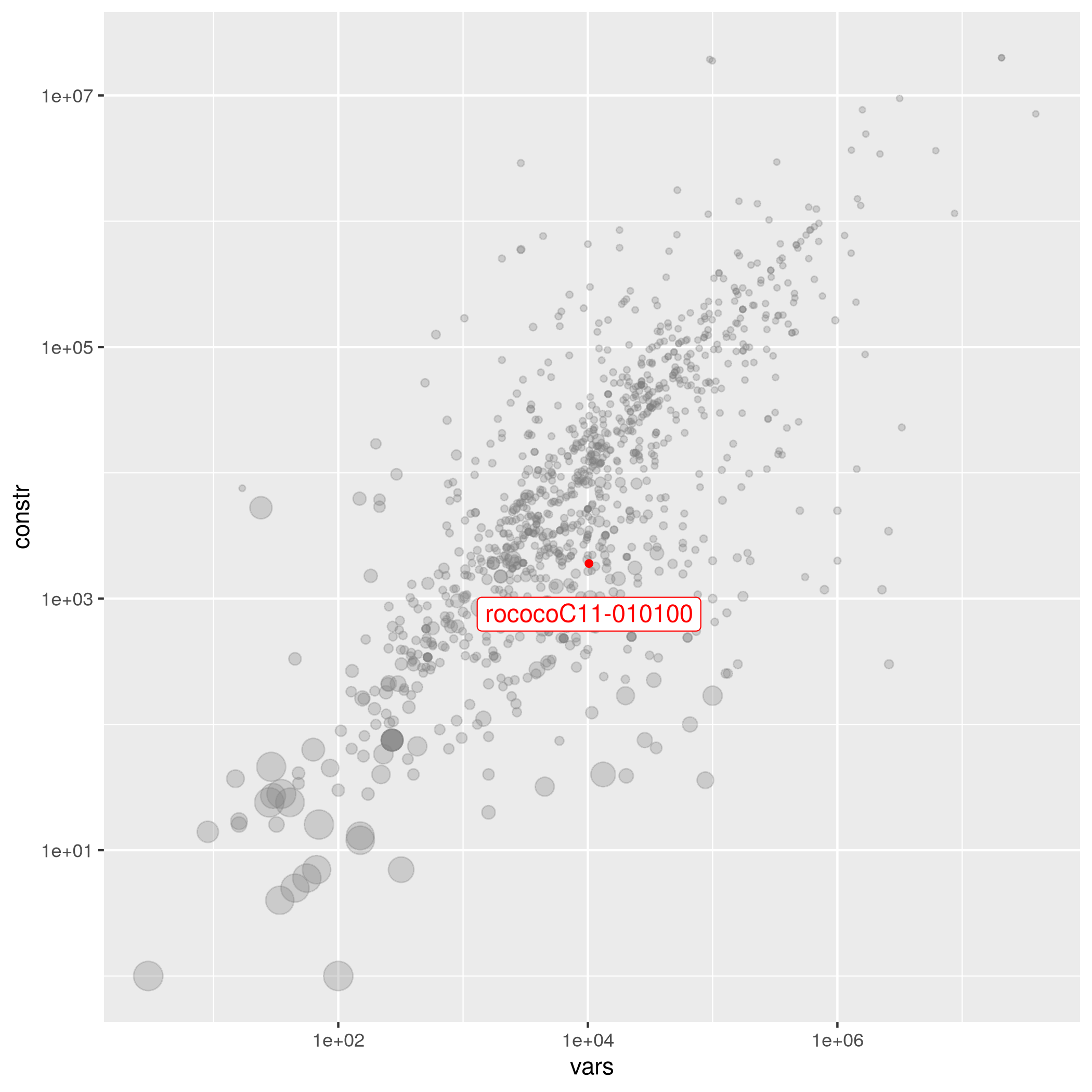
rococoC11-010100

decomposition aggregations precedence set_partitioning cardinality invariant_knapsack general_linear

Submitter	Variables	Constraints	Density	Status	Group	Objective	MPS File
A. Chabrier, E. Danna, C. Le Pape, L. Perron	12321	4010	9.50367e-04	hard	rococo	20889	rococoC11-010100.mps.gz

Model for dimensioning the arc capacities in a telecommunication network. Imported from the MIPLIB2010 submissions.

Location of instance in collection

Instance Statistics

Detailed explanation of the following tables can be found here.

Size Related Properties
	Original	Presolved
Variables	12321	10214
Constraints	4010	1902
Binaries	12155	10048
Integers	166	166
Continuous	0	0
Implicit Integers	0	0
Fixed Variables	0	0
Nonzero Density	0.000950367	0.002097230
Nonzeroes	46955	40743

Constraint Classification Properties
	Original	Presolved
Total	4010	1902
Empty	0	0
Free	0	0
Singleton	2108	0
Aggregations	220	220
Precedence	165	165
Variable Bound	0	0
Set Partitioning	216	216
Set Packing	0	0
Set Covering	0	0
Cardinality	972	972
Invariant Knapsack	108	108
Equation Knapsack	0	0
Bin Packing	0	0
Knapsack	0	0
Integer Knapsack	0	0
Mixed Binary	0	0
General Linear	221	221
Indicator	0	0

Structure

Available nonzero structure and decomposition information. Further information can be found here.

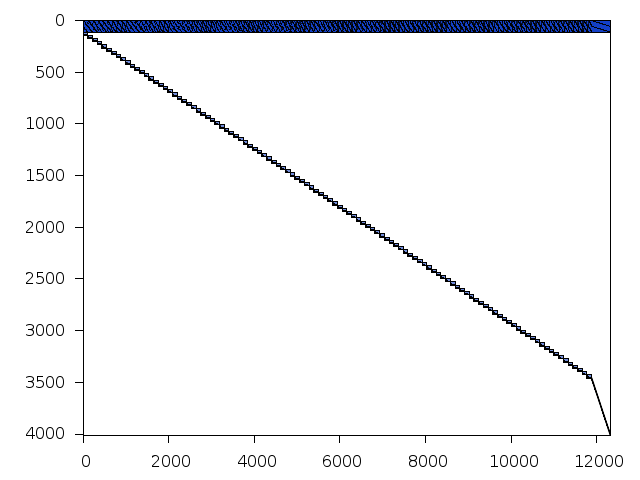
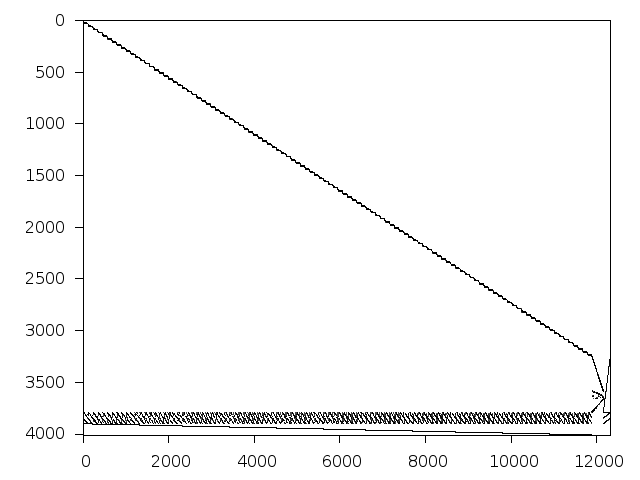
Nonzero entries of original problem

Nonzero entries after trivial presolving

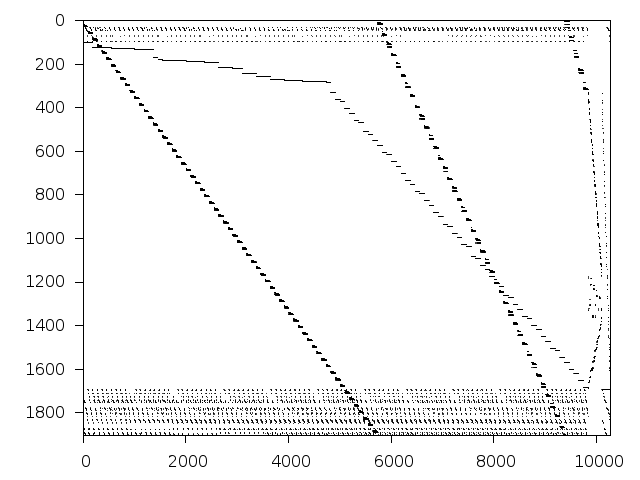
Decomposed structure of original problem (dec-file)

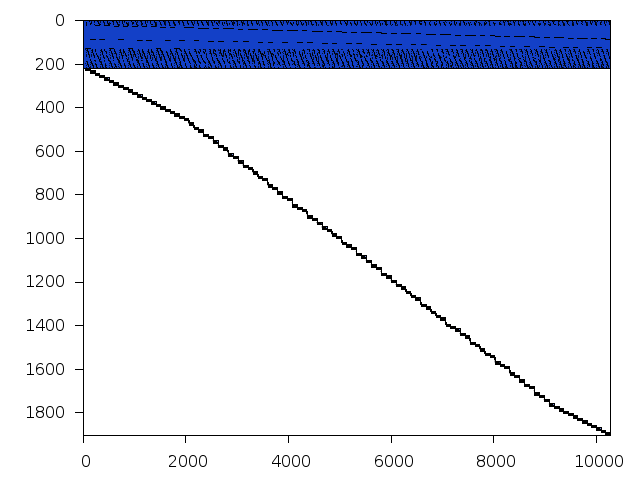
Decomposed structure after trivial presolving (dec-file)

	value	min	median	mean	max
Components	2.214844
Constraint %		0.4731860	0.573500	0.630915	0.630915
Variable %		0.0681663	0.610151	0.886162	0.886162
Score	0.928650

Best Known Solution(s)

Find solutions below. Download the archive containing all solutions from the Download page.

ID	Objective	Exact	Int. Viol	Cons. Viol	Obj. Viol	Submitter	Date	Description
2	20889	20889	0	0	0	Ishibashi Yasumi	2019-06-04	optimal solution as reported by ParaNUOPT after 32368 seconds using 9 cores in total
1	20889	20889	0	0	0	-	2018-10-11	Solution found during MIPLIB2017 problem selection.

Similar instances in collection

The following instances are most similar to rococoC11-010100 in the collection. This similarity analysis is based on 100 scaled instance features describing properties of the variables, objective function, bounds, constraints, and right hand sides.

Instance	Status	Variables	Binaries	Integers	Continuous	Constraints	Nonz.	Submitter	Group	Objective	Tags
rococoC11-011100	easy	6491	6325	166	0	2367	30472	A. Chabrier, E. Danna, C. Le Pape, L. Perron	rococo	20889	decomposition benchmark_suitable aggregations precedence set_partitioning cardinality invariant_knapsack general_linear
rococoB10-011000	easy	4456	4320	136	0	1667	16517	A. Chabrier, E. Danna, C. Le Pape, L. Perron	rococo	19449	benchmark decomposition benchmark_suitable precedence set_partitioning cardinality general_linear
rococoC12-010001	hard	16741	16554	187	0	4636	59832	A. Chabrier, E. Danna, C. Le Pape, L. Perron	rococo	34045.0	decomposition precedence set_partitioning cardinality knapsack general_linear
rococoC10-001000	easy	3117	2993	124	0	1293	11751	A. Chabrier, E. Danna, C. Le Pape, L. Perron	rococo	11460	benchmark benchmark_suitable precedence set_partitioning cardinality general_linear
qnet1_o	easy	1541	1288	129	124	456	4214	MIPLIB submission pool	–	16029.692681	decomposition aggregations precedence variable_bound set_partitioning cardinality general_linear

Reference

No bibliographic information available