MIPLIB 2017 – The Mixed Integer Programming Library
 In response to the needs of researchers for access to real-world
mixed integer programs, Robert E. Bixby, E.A. Boyd, and R.R. Indovina
created in 1992 the MIPLIB, an electronically available library of both
pure and mixed integer programs. Since its introduction, MIPLIB has
become a standard test set used to compare the performance of mixed
integer optimizers. Its availability has provided an important stimulus
for researchers in this very active area. The library has now been
released in its sixth edition as a collaborative effort between Arizona
State University, COIN-OR, CPLEX, FICO, Gurobi, MathWorks, MIPCL, MOSEK,
NUOPT, SAS, and Zuse Institute Berlin. Like the previous MIPLIB 2010,
two main sets have been compiled from the submissions. The Benchmark Set contains
240 instances that are solvable by (the union of) today’s codes. For
practical reasons, the benchmark instances were selected subject to
various constraints regarding solvability and numerical stability. The
much larger Collection
Set represents a diverse selection regardless of the above,
benchmark-relevant criteria. Download the instance sets as well as
supplementary data, run scripts and the solution checker from our Download page.
In response to the needs of researchers for access to real-world
mixed integer programs, Robert E. Bixby, E.A. Boyd, and R.R. Indovina
created in 1992 the MIPLIB, an electronically available library of both
pure and mixed integer programs. Since its introduction, MIPLIB has
become a standard test set used to compare the performance of mixed
integer optimizers. Its availability has provided an important stimulus
for researchers in this very active area. The library has now been
released in its sixth edition as a collaborative effort between Arizona
State University, COIN-OR, CPLEX, FICO, Gurobi, MathWorks, MIPCL, MOSEK,
NUOPT, SAS, and Zuse Institute Berlin. Like the previous MIPLIB 2010,
two main sets have been compiled from the submissions. The Benchmark Set contains
240 instances that are solvable by (the union of) today’s codes. For
practical reasons, the benchmark instances were selected subject to
various constraints regarding solvability and numerical stability. The
much larger Collection
Set represents a diverse selection regardless of the above,
benchmark-relevant criteria. Download the instance sets as well as
supplementary data, run scripts and the solution checker from our Download page.
Contact Us
The current maintainers of the website and its content are Ambros Gleixner and Julian Manns. Contributions of new solutions to open instances are always welcome, and will be made available in periodic updates of the web page. Also, we are happy to provide additional instance tags upon request.
Please send your submissions to miplibsolutions@zib.de
MIPLIB 2010
This page now hosts the new MIPLIB 2017. Find its predecessor MIPLIB 2010 on our Links page.
News & Status
News
| Apr 17, 2024 | Release of solufile 28 with 1 new optimal solution, 44 better incumbents and 30 instances updated from hard to easy. For instance pb-market-split8-70-4 we added a new optimal solution for the previously known optimal objective value. |
| Feb 29, 2024 | Release of solufile 27 with 1 new optimal solution and 4 better incumbents. For instance sorrell3 we added a new optimal solution for the previously known optimal objective value. |
| Jul 28, 2023 | Release of solufile 26 with 5 new optimal solutions and 34 better incumbents. Instance supportcase22 previously tagged infeasible was found feasible. Furthermore reverted generic to original variable names for the versions of glass4 and tr12-30 found in benchmark.zip and collection.zip. Replaced a wrong version of bley_xl1 that was provided for download on its instance page. |
| Nov 25, 2022 | Release of solufile 25 with 1 new optimal solution and 5 better incumbents. |
| Sep 28, 2022 | Release of solufile 24 with 7 better incumbents. |
Status
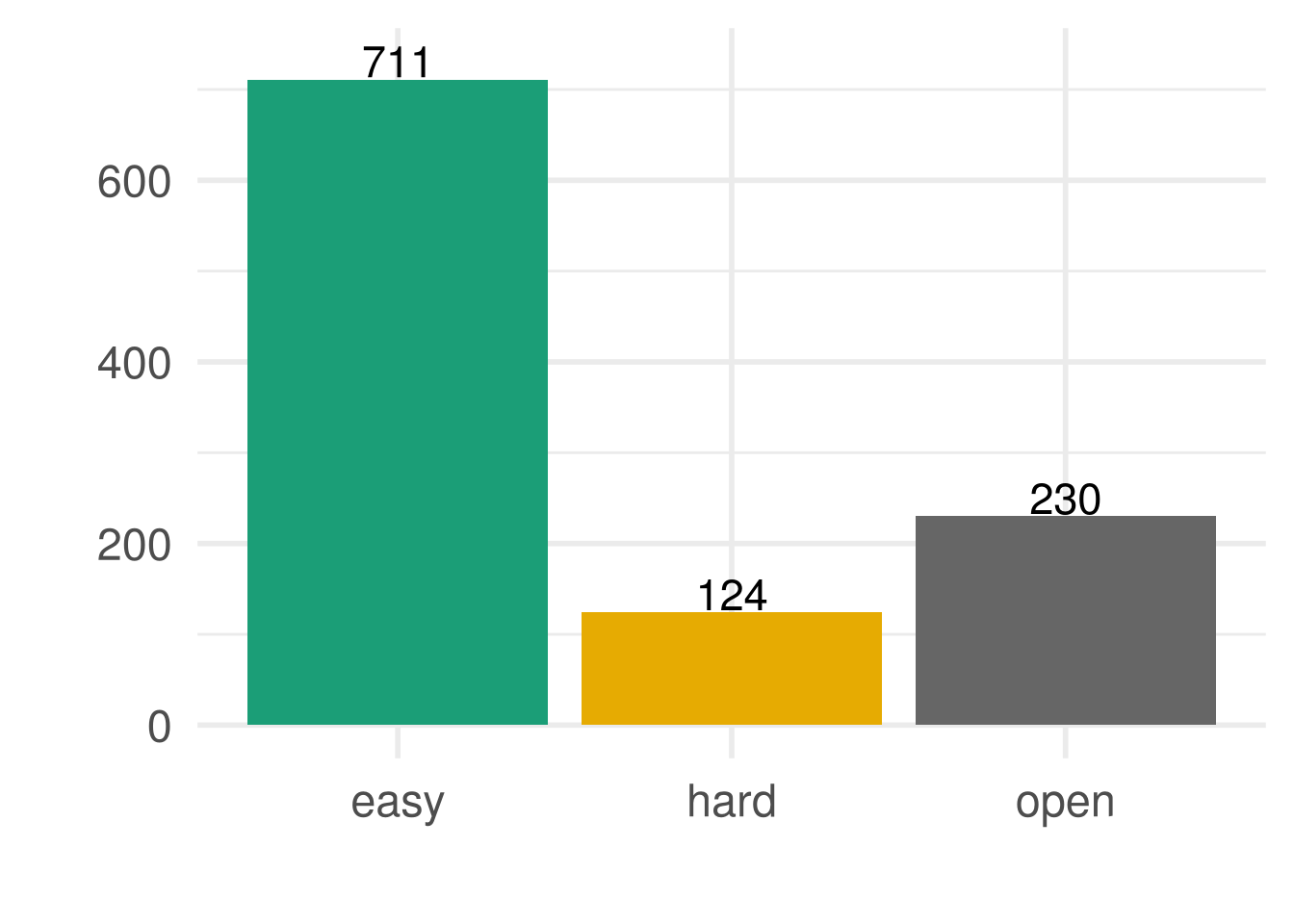
Frequencies of categories easy/hard/open
‘Easy’ means that the instance could be solved within less than one hour and with at most 16 threads, using an out-of-the-box solver on standard desktop computing hardware, ‘hard’ stands for instances, that have been solved in longer runs possibly using nonstandard hardware and/or algorithms, whereas ‘open’ means, that the instance has not yet been reported solved.
Citation
An article about the selection methodology has been published in Mathematical Programming Computation. Please cite MIPLIB 2017 as follows:
@article{
author = {Gleixner, Ambros and Hendel, Gregor and Gamrath, Gerald and Achterberg, Tobias and Bastubbe, Michael and Berthold, Timo and Christophel, Philipp M. and Jarck, Kati and Koch, Thorsten and Linderoth, Jeff and L\"ubbecke, Marco and Mittelmann, Hans D. and Ozyurt, Derya and Ralphs, Ted K. and Salvagnin, Domenico and Shinano, Yuji},
title = {{MIPLIB 2017: Data-Driven Compilation of the 6th Mixed-Integer Programming Library}},
journal = {Mathematical Programming Computation},
year = {2021},
doi = {10.1007/s12532-020-00194-3},
url = {https://doi.org/10.1007/s12532-020-00194-3}
}Disclaimer
Most of the data files on this site have been converted, some optimal solutions are gathered from papers and some data was typed in by hand or generated by automatic solution extraction programs. While we took every effort to make no mistakes, we cannot guarantee that everything is correct. If you find any errors or have doubts about a solution, please contact us.
Last Update 2024 by Julian Manns
generated with R Markdown
© by Zuse Institute Berlin (ZIB)
Imprint