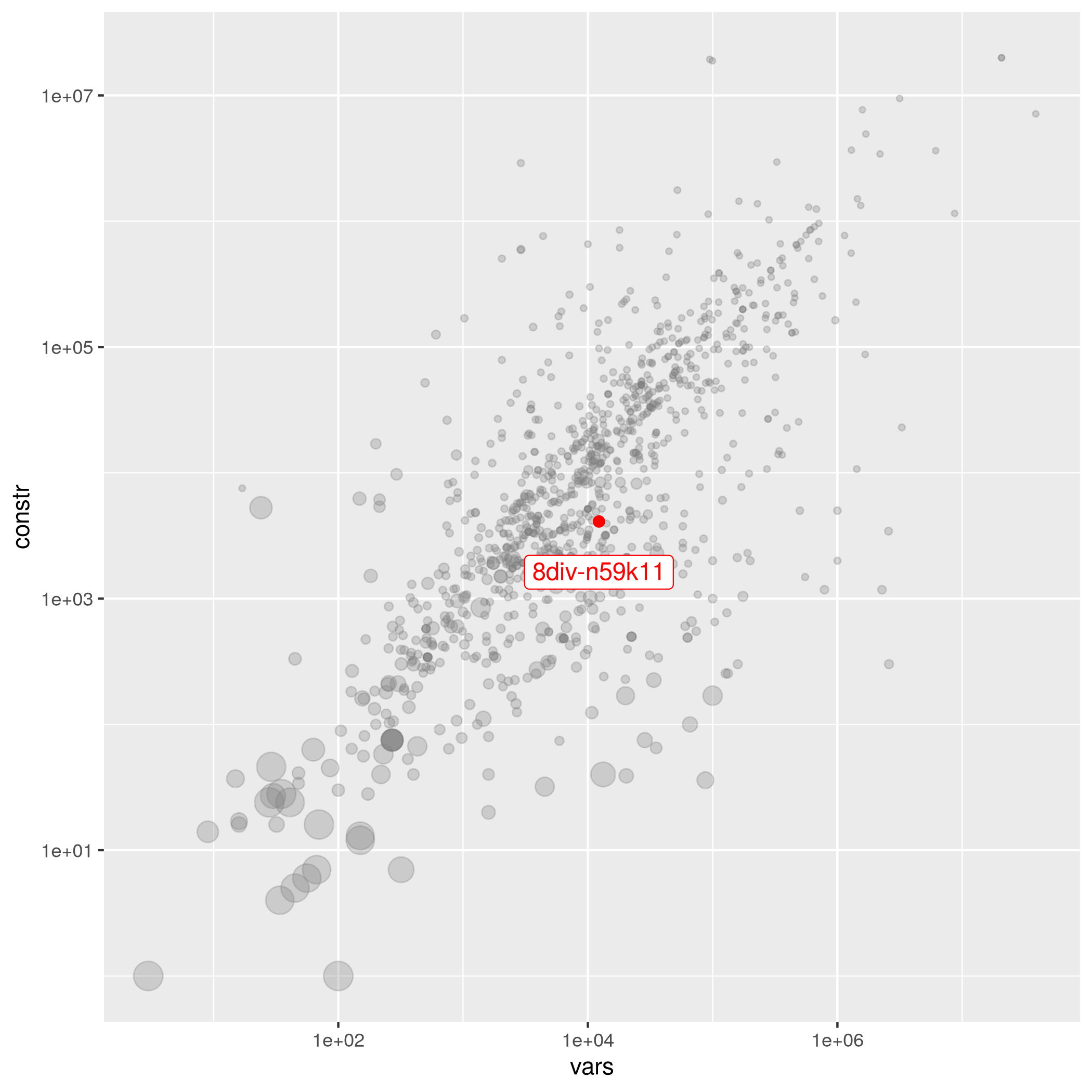
8div-n59k11

infeasible set_partitioning cardinality equation_knapsack integer_knapsack general_linear

Submitter	Variables	Constraints	Density	Status	Group	Objective	MPS File
Sascha Kurz	12287	4114	4.20755e-02	hard	8div	Infeasible	8div-n59k11.mps.gz

Projective binary 8-divisible linear block codes A linear block code is called 8-divisible if the weights of its codewords are divisible by 8. It is called projective if there are no duplicate columns in the generator matrix. The possible lengths of 8-divisible linear block codes have been classified except for length n=59, where it is undecided whether such a linear code exists. The possible dimensions satisfy \(10 \le k \le 20\). Instance 8div_n59_kXX contains the corresponding feasibility problem. Projective binary 8-divisible linear block codes occur as hole configurations of so-called partial solid spreads in finite geometry. Binary 4-divisible linear block codes have applications in physics.

Location of instance in collection

Instance Statistics

Detailed explanation of the following tables can be found here.

Size Related Properties
	Original	Presolved
Variables	12287	12276
Constraints	4114	4103
Binaries	12282	12271
Integers	5	5
Continuous	0	0
Implicit Integers	0	0
Fixed Variables	0	0
Nonzero Density	0.0420755	0.0420023
Nonzeroes	2126860	2115590

Constraint Classification Properties
	Original	Presolved
Total	4117	4106
Empty	0	0
Free	0	0
Singleton	11	0
Aggregations	0	0
Precedence	0	0
Variable Bound	0	0
Set Partitioning	2047	2047
Set Packing	0	0
Set Covering	0	0
Cardinality	1	1
Invariant Knapsack	0	0
Equation Knapsack	2047	2047
Bin Packing	0	0
Knapsack	0	0
Integer Knapsack	3	3
Mixed Binary	0	0
General Linear	8	8
Indicator	0	0

Structure

Available nonzero structure and decomposition information. Further information can be found here.

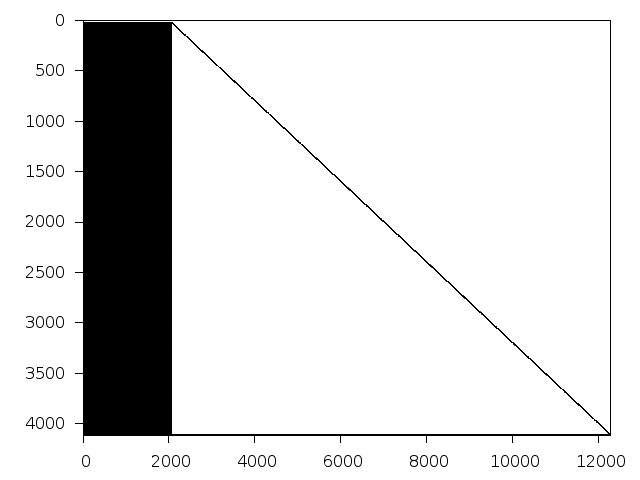
Nonzero entries of original problem

Nonzero entries after trivial presolving

Decomposed structure of original problem (dec-file)

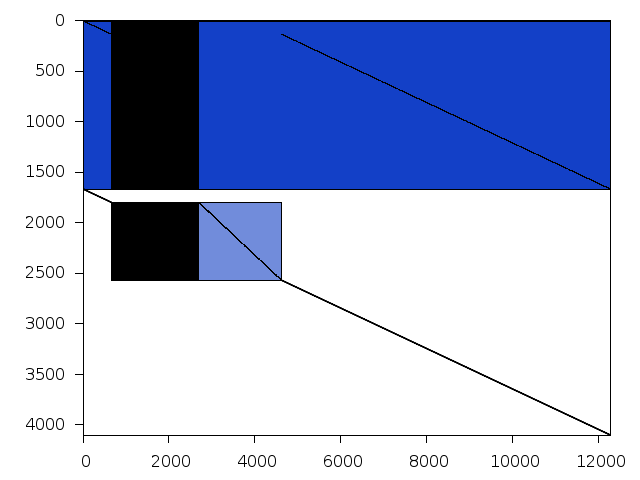
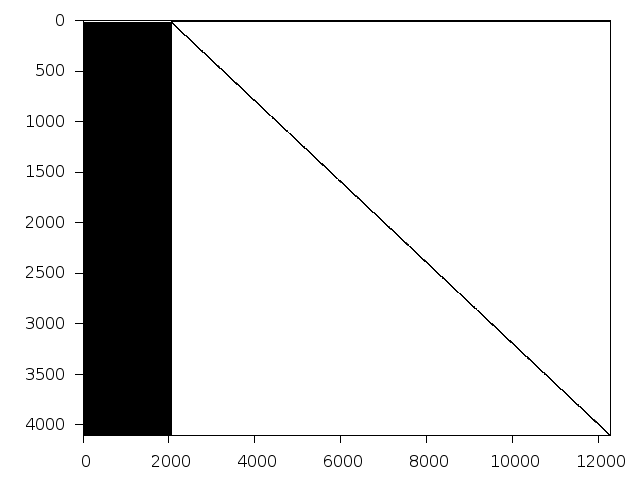
Decomposed structure after trivial presolving (dec-file)

	value	min	median	mean	max
Components	3.221414
Constraint %		0.0243724	0.0356652	0.0243724	18.7668
Variable %		0.0406934	0.0600375	0.0406934	32.2292
Score	0.532819

Best Known Solution(s)

No solution available for 8div-n59k11 .

Similar instances in collection

The following instances are most similar to 8div-n59k11 in the collection. This similarity analysis is based on 100 scaled instance features describing properties of the variables, objective function, bounds, constraints, and right hand sides.

Instance	Status	Variables	Binaries	Integers	Constraints	Nonz.	Submitter	Group	Objective	Tags
8div-n59k10	hard	6143	6138	5	2065	539151	Sascha Kurz	8div	Infeasible	infeasible set_partitioning cardinality equation_knapsack integer_knapsack general_linear
8div-n59k12	hard	24575	24570	5	8211	8448017	Sascha Kurz	8div	Infeasible	infeasible set_partitioning cardinality equation_knapsack integer_knapsack general_linear
neos-3045796-mogo	easy	11016	11016	0	2226	44442	Jeff Linderoth	neos-pseudoapplication-22	-175	binary decomposition set_partitioning set_packing set_covering invariant_knapsack equation_knapsack
neos-952987	hard	31329	31329	0	354	90384	NEOS Server Submission	neos-pseudoapplication-22	Infeasible	infeasible binary set_covering equation_knapsack knapsack
highschool1-aigio	hard	320404	319686	718	92568	1562168	George Fonseca	timetabling	0	benchmark benchmark_suitable aggregations variable_bound set_partitioning set_packing set_covering cardinality invariant_knapsack equation_knapsack general_linear

Reference

@incollection{ubt_eref40887,
          author = {Daniel Heinlein and Thomas Honold and Michael Kiermaier and Sascha Kurz and Alfred Wassermann},
       booktitle = {The Tenth International Workshop on Coding and Cryptography 2017 : WCC Proceedings},
         address = {Saint-Petersburg},
           month = {September},
           title = {Projective divisible binary codes},
            year = {2017},
             url = {https://eref.uni-bayreuth.de/40887/},
        keywords = {divisible codes; projective codes; partial spreads}
}

@article{heinlein2017classifying,
  title   =  {Classifying optimal binary subspace codes of length 8, constant dimension 4 and minimum distance 6},
  author  =  {Heinlein, Daniel and Honold, Thomas and Kiermaier, Michael and Kurz, Sascha and Wassermann, Alfred},
  journal =  {Designs, Codes and Cryptography},
  note    =  {arXiv preprint arXiv:1711.06624},
  year    =  {to appear},
  doi     =  {10.1007/s10623-018-0544-8}
}