a2864-99blp

binary set_packing invariant_knapsack

Submitter	Variables	Constraints	Density	Status	Group	Objective	MPS File
Daniel Heinlein	200787	22117	4.52141e-03	open	selofsubspaces	-257*	a2864-99blp.mps.gz

Clique problems arising from a selection problem of subspaces in the PG(7,2) with different prescribed variables and numerically instable linear programming relaxation.

Location of instance in collection

Instance Statistics

Detailed explanation of the following tables can be found here.

Size Related Properties
	Original	Presolved
Variables	200787	13824
Constraints	22117	20893
Binaries	200787	13824
Integers	0	0
Continuous	0	0
Implicit Integers	0	0
Fixed Variables	0	0
Nonzero Density	0.00452141	0.00478629
Nonzeroes	20078700	1382400

Constraint Classification Properties
	Original	Presolved
Total	22117	20893
Empty	0	0
Free	0	0
Singleton	17	0
Aggregations	0	0
Precedence	0	0
Variable Bound	0	0
Set Partitioning	0	0
Set Packing	21590	20384
Set Covering	0	0
Cardinality	0	0
Invariant Knapsack	510	509
Equation Knapsack	0	0
Bin Packing	0	0
Knapsack	0	0
Integer Knapsack	0	0
Mixed Binary	0	0
General Linear	0	0
Indicator	0	0

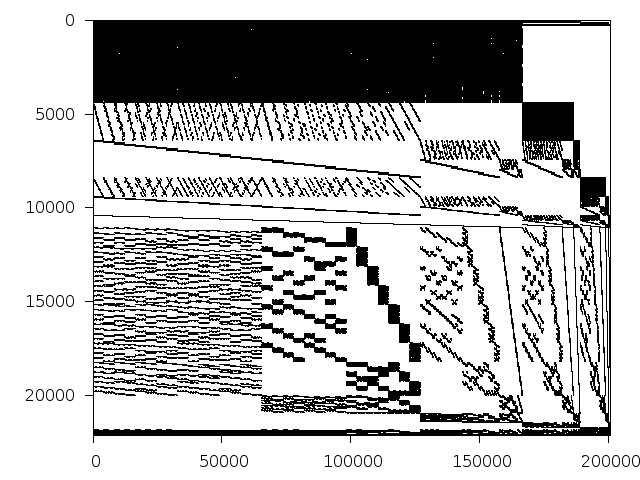
Structure

Available nonzero structure and decomposition information. Further information can be found here.

Nonzero entries of original problem

Nonzero entries after trivial presolving

Decomposed structure of original problem (dec-file)

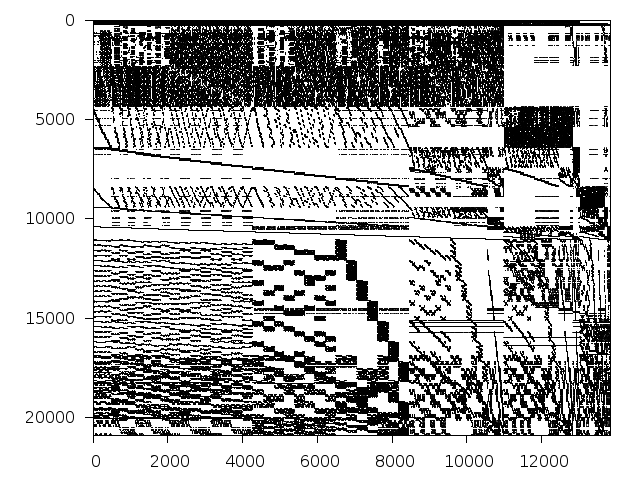
Decomposed structure after trivial presolving (dec-file)

	value	min	median	mean	max
Components	0.301030
Constraint %		100.0000	100.0000	100.0000	100.0000
Variable %		99.8772	99.8772	99.8772	99.8772
Score	0.001228

Best Known Solution(s)

Find solutions below. Download the archive containing all solutions from the Download page.

ID	Objective	Exact	Int. Viol	Cons. Viol	Obj. Viol	Submitter	Date	Description
1	-257	-257	0	0	0	-	2018-10-13	Solution found during MIPLIB2017 problem selection.

Similar instances in collection

The following instances are most similar to a2864-99blp in the collection. This similarity analysis is based on 100 scaled instance features describing properties of the variables, objective function, bounds, constraints, and right hand sides.

Instance	Status	Variables	Binaries	Constraints	Nonz.	Submitter	Group	Objective	Tags
cdc7-4-3-2	open	11811	11811	14478	259842	Sascha Kurz	–	-296.0*	binary set_packing
cod105	easy	1024	1024	1024	57344	MIPLIB submission pool	–	-12	benchmark binary benchmark_suitable set_packing
z26	open	17937	17937	850513	1715613	Daniel Bienstock	–	-1195.0*	binary variable_bound set_packing
sorrell7	open	2048	2048	78848	157696	Toni Sorrell	independentset	-198.0*	binary variable_bound
sorrell3	easy	1024	1024	169162	338324	Toni Sorrell	independentset	-16	benchmark binary benchmark_suitable variable_bound

Reference

@article{honold2016classification,
    title   =  {Classification of large partial plane spreads in ${PG}(6, 2)$ and related combinatorial objects},
    author  =  {Honold, Thomas and Kiermaier, Michael and Kurz, Sascha},
    journal =  {Journal of Geometry},
    note    =  {arXiv preprint arXiv:1606.07655},
    year    =  {to appear}
}