acc-tight4

binary benchmark_suitable precedence set_partitioning set_packing set_covering cardinality invariant_knapsack mixed_binary

Submitter	Variables	Constraints	Density	Status	Group	Objective	MPS File
J. Walser	1620	3285	3.20819e-03	easy	acc-tight	0	acc-tight4.mps.gz

ACC basketball scheduling instance Imported from MIPLIB2010.

Location of instance in collection

Instance Statistics

Detailed explanation of the following tables can be found here.

Size Related Properties
	Original	Presolved
Variables	1620	1620
Constraints	3285	3285
Binaries	1620	1620
Integers	0	0
Continuous	0	0
Implicit Integers	0	0
Fixed Variables	0	0
Nonzero Density	0.00320819	0.00320819
Nonzeroes	17073	17073

Constraint Classification Properties
	Original	Presolved
Total	3285	3285
Empty	0	0
Free	0	0
Singleton	0	0
Aggregations	0	0
Precedence	2025	2025
Variable Bound	0	0
Set Partitioning	261	261
Set Packing	162	162
Set Covering	9	198
Cardinality	36	36
Invariant Knapsack	783	594
Equation Knapsack	0	0
Bin Packing	0	0
Knapsack	0	0
Integer Knapsack	0	0
Mixed Binary	9	9
General Linear	0	0
Indicator	0	0

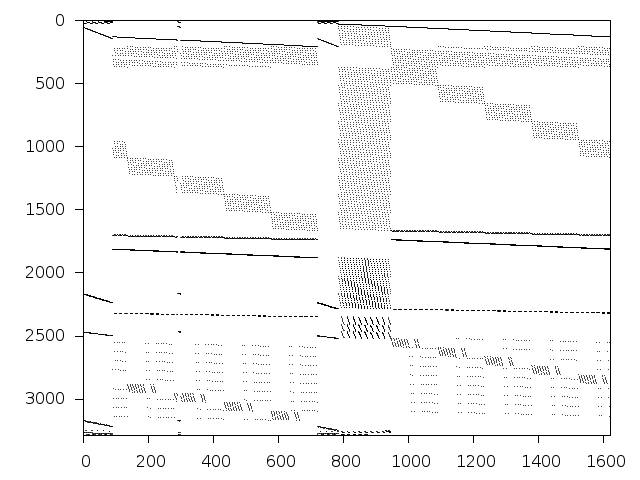
Structure

Available nonzero structure and decomposition information. Further information can be found here.

Nonzero entries of original problem

Nonzero entries after trivial presolving

Decomposed structure of original problem (dec-file)

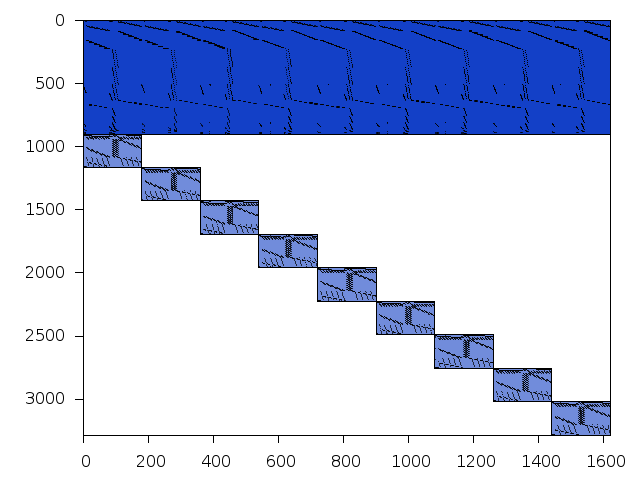
Decomposed structure after trivial presolving (dec-file)

	value	min	median	mean	max
Components	1.959041
Constraint %		0.0304414	0.739726	0.0304414	7.12329
Variable %		0.1234570	1.111110	0.1234570	10.00000
Score	0.601613

Best Known Solution(s)

Find solutions below. Download the archive containing all solutions from the Download page.

ID	Objective	Exact	Int. Viol	Cons. Viol	Obj. Viol	Submitter	Date	Description
1	0	0	0	0	0	-	2018-10-11	Solution found during MIPLIB2017 problem selection.

Similar instances in collection

The following instances are most similar to acc-tight4 in the collection. This similarity analysis is based on 100 scaled instance features describing properties of the variables, objective function, bounds, constraints, and right hand sides.

Instance	Status	Variables	Binaries	Continuous	Constraints	Nonz.	Submitter	Group	Objective	Tags
acc-tight5	easy	1339	1339	0	3052	16134	J. Walser	acc-tight	0	binary benchmark_suitable aggregations precedence variable_bound set_partitioning set_packing set_covering cardinality invariant_knapsack mixed_binary
acc-tight2	easy	1620	1620	0	2520	15327	J. Walser	acc-tight	0	binary benchmark_suitable precedence set_partitioning set_packing set_covering cardinality invariant_knapsack
neos-1330346	easy	2664	2664	0	4248	13032	NEOS Server Submission	neos-pseudoapplication-49	8	binary decomposition benchmark_suitable aggregations precedence variable_bound cardinality
neos18	easy	3312	3312	0	11402	24614	NEOS Server Submission	neos-pseudoapplication-49	16	binary decomposition benchmark_suitable precedence variable_bound set_covering invariant_knapsack
physiciansched6-2	easy	111827	109346	2481	168336	480259	Pelin Damci-Kurt	physiciansched	49324	benchmark decomposition benchmark_suitable precedence variable_bound set_packing set_covering invariant_knapsack binpacking knapsack mixed_binary

Reference

@article{NemhauserTrick1998,
 author = {G. L. Nemhauser and M. A. Trick},
 journal = {Operations Research},
 language = {English},
 number = {1},
 pages = {1--8},
 title = {Scheduling a Major College Basketball Conference},
 volume = {46},
 year = {1998}
}

@misc{Walser1998,
 author = {J. P. Walser},
 note = {http://www.ps.uni-saarland.de/~walser/acc/acc.html},
 title = {Solving the {ACC} Basketball Scheduling Problem with Integer Local
Search},
 year = {1998}
}