adult-regularized

variable_bound general_linear

Submitter	Variables	Constraints	Density	Status	Group	Objective	MPS File
Berk Ustun	32674	32709	3.90712e-04	open	ustun	7022.953543477999*	adult-regularized.mps.gz

MIP to create optimized data-driven scoring systems. See: https://github.com/ustunb/miplib2017-slim#miplib2017-slim for a description.

Location of instance in collection

Instance Statistics

Detailed explanation of the following tables can be found here.

Size Related Properties
	Original	Presolved
Variables	32674	32674
Constraints	32709	32709
Binaries	32597	32597
Integers	41	41
Continuous	36	36
Implicit Integers	0	0
Fixed Variables	0	0
Nonzero Density	0.000390712	0.000390712
Nonzeroes	417567	417567

Constraint Classification Properties
	Original	Presolved
Total	32709	32709
Empty	0	0
Free	0	0
Singleton	0	0
Aggregations	0	0
Precedence	0	0
Variable Bound	144	144
Set Partitioning	0	0
Set Packing	0	0
Set Covering	0	0
Cardinality	0	0
Invariant Knapsack	0	0
Equation Knapsack	0	0
Bin Packing	0	0
Knapsack	0	0
Integer Knapsack	0	0
Mixed Binary	0	0
General Linear	32565	32565
Indicator	0	0

Structure

Available nonzero structure and decomposition information. Further information can be found here.

Nonzero entries of original problem

Nonzero entries after trivial presolving

Decomposed structure of original problem (dec-file)

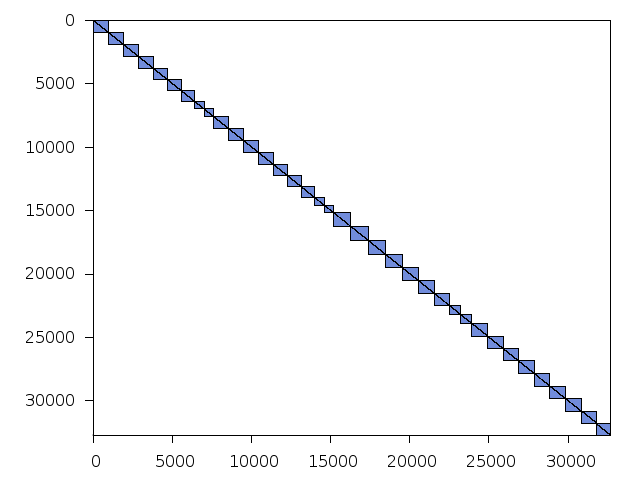
Decomposed structure after trivial presolving (dec-file)

	value	min	median	mean	max
Components	1.568202
Constraint %		0.0122291	0.0122291	0.0122291	0.0122291
Variable %		0.0091800	0.0091800	0.0091800	0.0091800
Score	0.004402

Best Known Solution(s)

Find solutions below. Download the archive containing all solutions from the Download page.

ID	Objective	Exact	Int. Viol	Cons. Viol	Obj. Viol	Submitter	Date	Description
1	7022.954	7022.954	0	0	0	-	2018-10-11	Solution found during MIPLIB2017 problem selection.

Similar instances in collection

The following instances are most similar to adult-regularized in the collection. This similarity analysis is based on 100 scaled instance features describing properties of the variables, objective function, bounds, constraints, and right hand sides.

Instance	Status	Variables	Binaries	Integers	Continuous	Constraints	Nonz.	Submitter	Group	Objective	Tags
breastcancer-regularized	easy	715	692	14	9	723	8283	Berk Ustun	ustun	35.76784210526315	numerics variable_bound general_linear
adult-max5features	hard	32674	32597	41	36	32709	417567	Berk Ustun	ustun	5642.121938895418	variable_bound general_linear
mushroom-best	easy	8468	8237	118	113	8580	188735	Berk Ustun	ustun	0.0553337612	benchmark benchmark_suitable variable_bound general_linear
neos-1456979	easy	4605	4245	180	180	6770	36440	NEOS Server Submission	neos-pseudoapplication-102	176	benchmark decomposition benchmark_suitable variable_bound set_partitioning set_packing cardinality knapsack mixed_binary general_linear
supportcase33	easy	20203	20102	101	0	20489	211915	Domenico Salvagnin	–	-345	benchmark benchmark_suitable precedence variable_bound set_partitioning set_packing cardinality invariant_knapsack knapsack integer_knapsack general_linear

Reference

@article{
    ustun2015slim,
    year = {2015},
    issn = {0885-6125},
    journal = {Machine Learning},
    doi = {10.1007/s10994-015-5528-6},
    title = {Supersparse linear integer models for optimized medical scoring systems},
    url = {http://dx.doi.org/10.1007/s10994-015-5528-6},
    publisher = { Springer US},
    author = {Ustun, Berk and Rudin, Cynthia},
    pages = {1-43},
    language = {English}
}