bnatt500

benchmark infeasible binary benchmark_suitable precedence set_covering invariant_knapsack binpacking knapsack

Submitter	Variables	Constraints	Density	Status	Group	Objective	MPS File
Tatsuya Akutsu	4500	7029	8.60024e-04	easy	bnatt	Infeasible	bnatt500.mps.gz

We are submitting ILP data for identification of a singletonattractor in a Boolean newtork, which is a well-known problemin computational systems biology.This problem is known to be NP-hard and we developed a methodto transform an instance of the problem to an integer linearprogram (ILP).We used ILPs from artificially generated Boolean networks ofindegree 3.The size of the networks are: 350, 400, 500.Even for the case of 500, we could not find a solution within6 hours using CPLEX 11.2 on a PC with XEON 5470 3.33GHz CPU.(This ILP corresponds to the case of size=350.File format is (zipped) CPLEX LP format.)The details of the method appeared in:T. Akutsu, M. Hayashida and T. Tamura, Integer programming-basedmethods for attractor detection and control of Boolean networks,Proc. The combined 48th IEEE Conference on Decision and Controland 28th Chinese Control Conference (IEEE CDC/CCC 2009), 5610-5617, 2009. Imported from the MIPLIB2010 submissions. Solved with COPT 7.0 using up to 12 threads in less than 30 minutes.

Location of instance in collection

Instance Statistics

Detailed explanation of the following tables can be found here.

Size Related Properties
	Original	Presolved
Variables	4500	2529
Constraints	7029	5058
Binaries	4500	2529
Integers	0	0
Continuous	0	0
Implicit Integers	0	0
Fixed Variables	0	0
Nonzero Density	0.000860024	0.001664360
Nonzeroes	27203	21290

Constraint Classification Properties
	Original	Presolved
Total	7029	5058
Empty	0	0
Free	0	0
Singleton	1971	0
Aggregations	0	0
Precedence	0	24
Variable Bound	0	0
Set Partitioning	0	0
Set Packing	0	0
Set Covering	2029	260
Cardinality	0	0
Invariant Knapsack	500	2257
Equation Knapsack	0	0
Bin Packing	0	488
Knapsack	0	2029
Integer Knapsack	0	0
Mixed Binary	2529	0
General Linear	0	0
Indicator	0	0

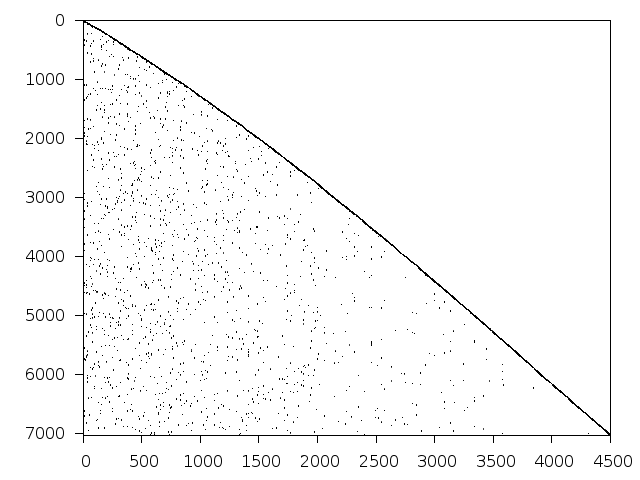
Structure

Available nonzero structure and decomposition information. Further information can be found here.

Nonzero entries of original problem

Nonzero entries after trivial presolving

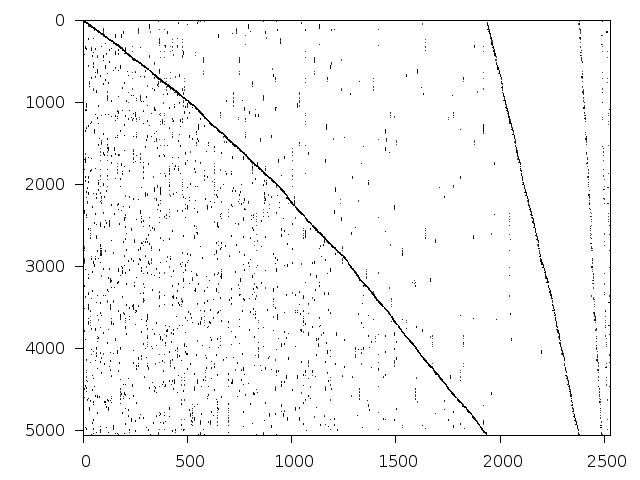
Decomposed structure of original problem (dec-file)

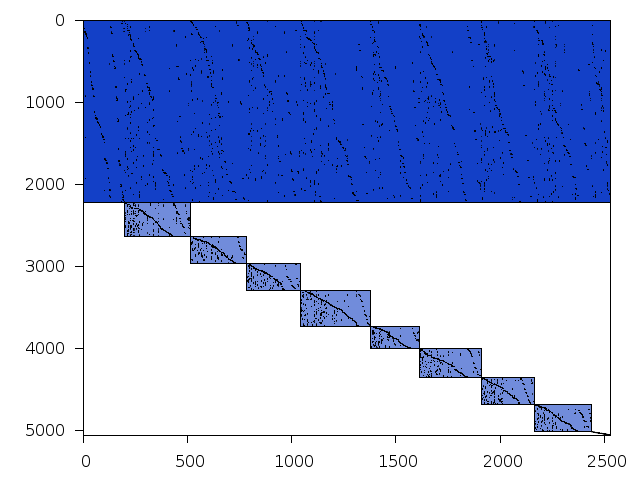
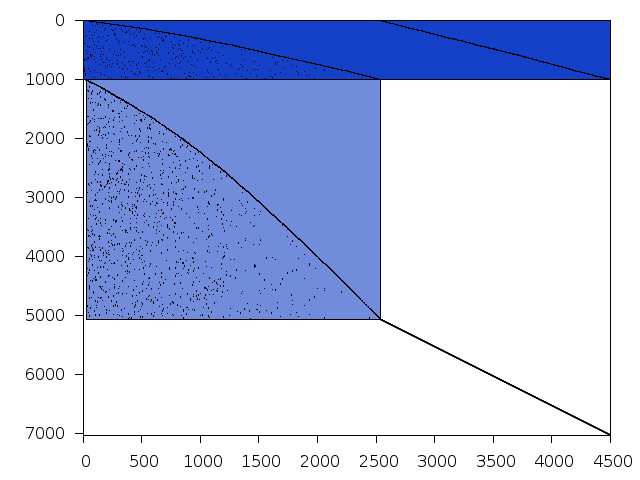
Decomposed structure after trivial presolving (dec-file)

	value	min	median	mean	max
Components	2.589950
Constraint %		0.0395413	0.0395413	0.0395413	0.0395413
Variable %		0.0790826	0.2120760	0.1977070	0.3558720
Score	0.153095

Best Known Solution(s)

No solution available for bnatt500 .

Similar instances in collection

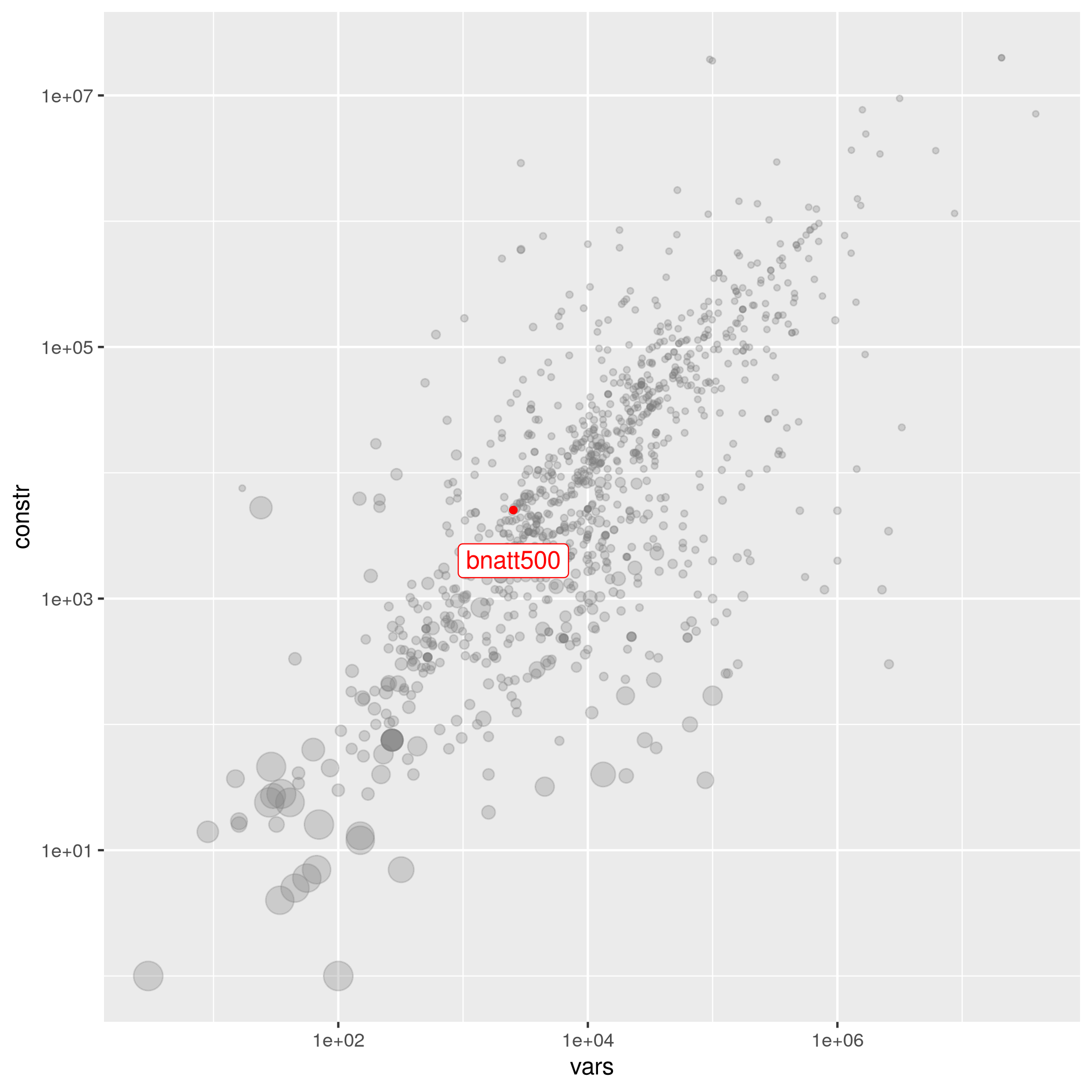
The following instances are most similar to bnatt500 in the collection. This similarity analysis is based on 100 scaled instance features describing properties of the variables, objective function, bounds, constraints, and right hand sides.

Instance	Status	Variables	Binaries	Continuous	Constraints	Nonz.	Submitter	Group	Objective	Tags
bnatt400	easy	3600	3600	0	5614	21698	Tatsuya Akutsu	bnatt	1	benchmark binary benchmark_suitable precedence set_covering invariant_knapsack binpacking knapsack
s1234	hard	2945	2945	0	8418	44641	Siwei Sun	SiweiSun	29	binary precedence set_covering invariant_knapsack binpacking knapsack
neos-5178119-nalagi	easy	4167	4068	99	6921	74476	Jeff Linderoth	neos-pseudoapplication-62	22.73999999763	benchmark_suitable precedence set_partitioning set_packing set_covering cardinality invariant_knapsack knapsack mixed_binary general_linear
circ10-3	open	2700	2700	0	42620	307320	M. Winkler	–	258.0*	binary decomposition precedence variable_bound set_partitioning set_packing invariant_knapsack knapsack mixed_binary
supportcase3	easy	4191	4191	0	12702	53470	Michael Winkler	–	0	binary feasibility aggregations precedence variable_bound invariant_knapsack knapsack mixed_binary

Reference

No bibliographic information available