chromaticindex32-8

binary benchmark_suitable set_partitioning set_packing

Submitter	Variables	Constraints	Density	Status	Group	Objective	MPS File
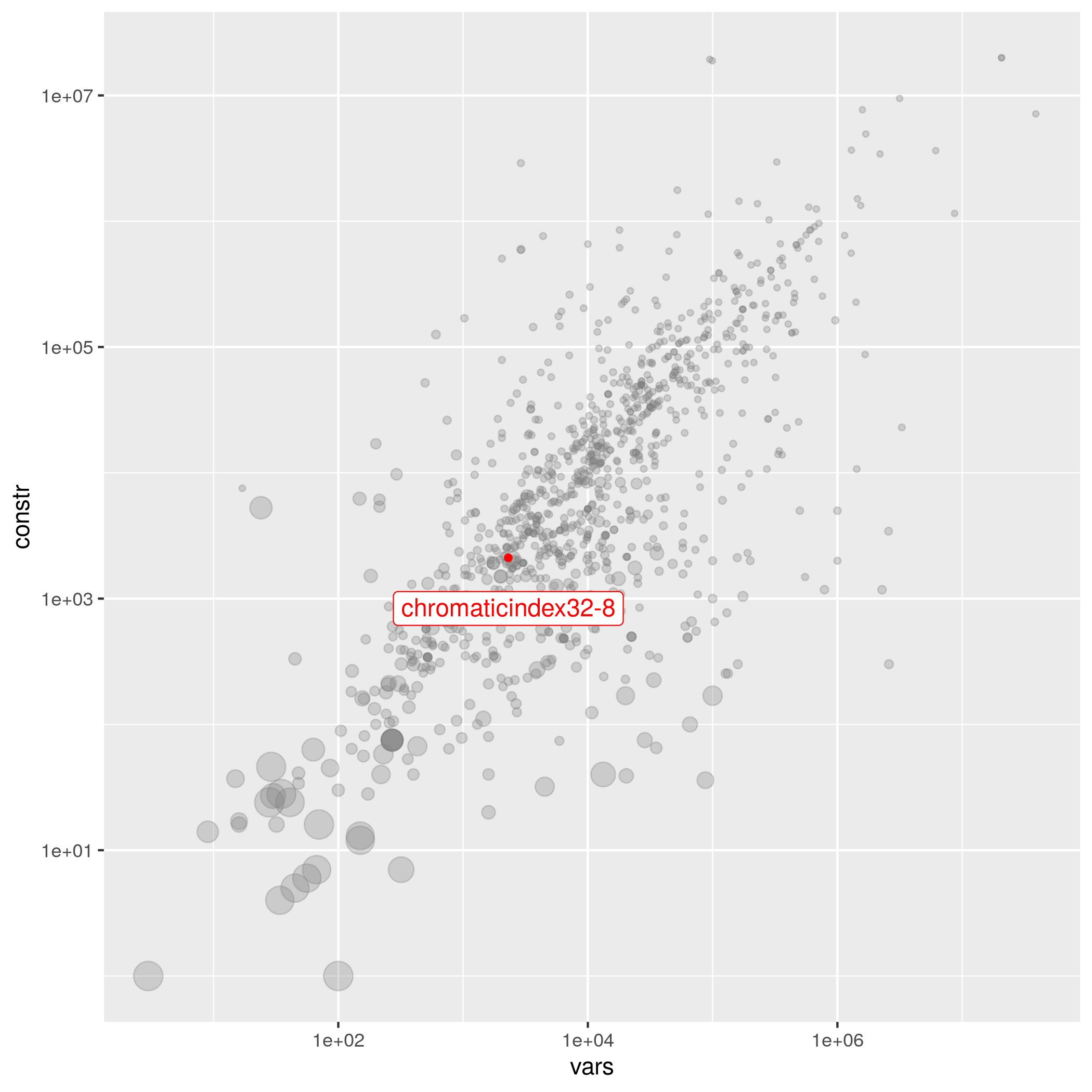
Pierre Le Bodic	2304	2111	1.73447e-03	easy	chromaticindex	4	chromaticindex32-8.mps.gz

Simple edge-coloring model on chains of Petersen-like subgraphs, designed to fool MIP solvers into producing very large Branch-and-Bound trees.

Location of instance in collection

Instance Statistics

Detailed explanation of the following tables can be found here.

Size Related Properties
	Original	Presolved
Variables	2304	2304
Constraints	2111	2111
Binaries	2304	2304
Integers	0	0
Continuous	0	0
Implicit Integers	0	0
Fixed Variables	0	0
Nonzero Density	0.00173447	0.00173447
Nonzeroes	8436	8436

Constraint Classification Properties
	Original	Presolved
Total	2111	2111
Empty	0	0
Free	0	0
Singleton	0	0
Aggregations	0	0
Precedence	0	0
Variable Bound	0	0
Set Partitioning	575	575
Set Packing	1536	1536
Set Covering	0	0
Cardinality	0	0
Invariant Knapsack	0	0
Equation Knapsack	0	0
Bin Packing	0	0
Knapsack	0	0
Integer Knapsack	0	0
Mixed Binary	0	0
General Linear	0	0
Indicator	0	0

Structure

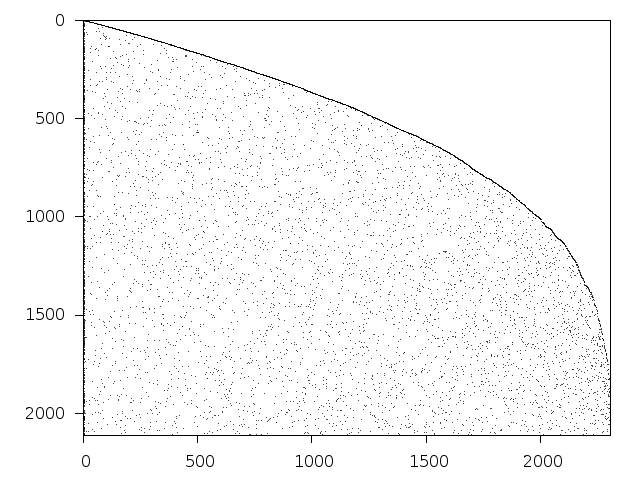
Available nonzero structure and decomposition information. Further information can be found here.

Nonzero entries of original problem

Nonzero entries after trivial presolving

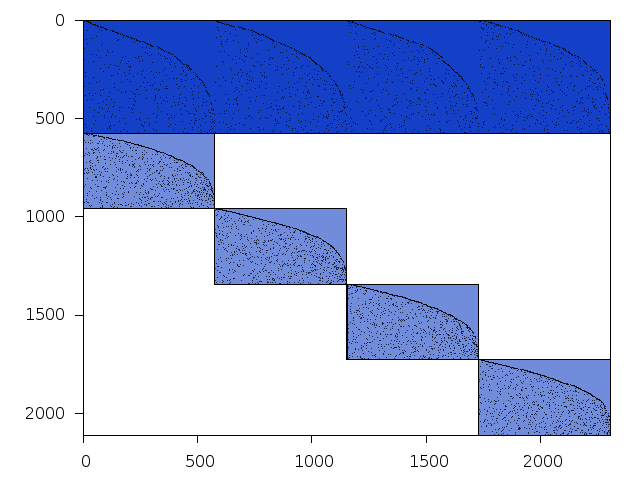
Decomposed structure of original problem (dec-file)

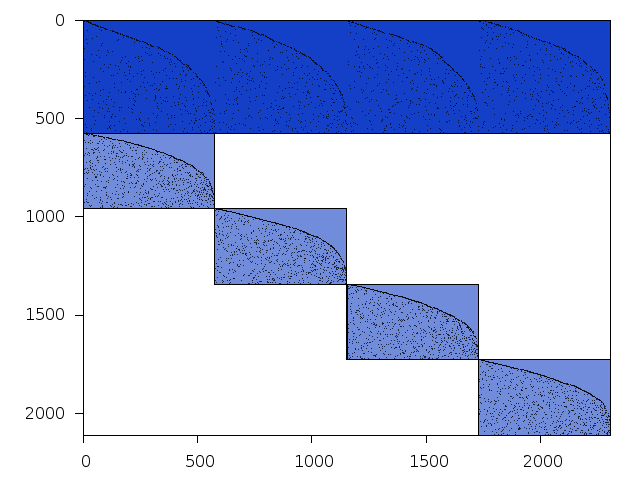
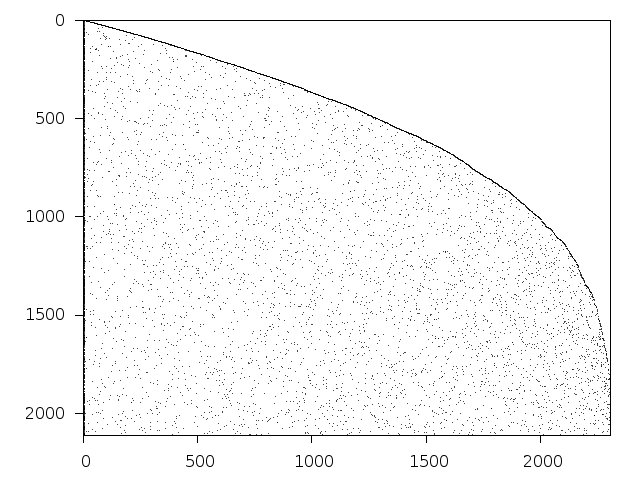
Decomposed structure after trivial presolving (dec-file)

	value	min	median	mean	max
Components	0.698970
Constraint %		18.1904	18.1904	18.1904	18.1904
Variable %		25.0000	25.0000	25.0000	25.0000
Score	0.545713

Best Known Solution(s)

Find solutions below. Download the archive containing all solutions from the Download page.

ID	Objective	Exact	Int. Viol	Cons. Viol	Obj. Viol	Submitter	Date	Description
1	4	4	0	0	0	-	2018-10-13	Solution found during MIPLIB2017 problem selection.

Similar instances in collection

The following instances are most similar to chromaticindex32-8 in the collection. This similarity analysis is based on 100 scaled instance features describing properties of the variables, objective function, bounds, constraints, and right hand sides.

Instance	Status	Variables	Binaries	Continuous	Constraints	Nonz.	Submitter	Group	Objective	Tags
chromaticindex128-5	easy	9216	9216	0	8447	33780	Pierre Le Bodic	chromaticindex	4	binary benchmark_suitable set_partitioning set_packing
chromaticindex256-8	easy	18432	18432	0	16895	67572	Pierre Le Bodic	chromaticindex	4	binary benchmark_suitable set_partitioning set_packing
chromaticindex512-7	easy	36864	36864	0	33791	135156	Pierre Le Bodic	chromaticindex	4	benchmark binary benchmark_suitable set_partitioning set_packing
chromaticindex1024-7	easy	73728	73728	0	67583	270324	Pierre Le Bodic	chromaticindex	4	benchmark binary benchmark_suitable set_partitioning set_packing
neos-691058	easy	3006	1755	1251	2667	30837	NEOS Server Submission	neos-pseudoapplication-110	296.999999999986	benchmark_suitable set_partitioning cardinality mixed_binary

Reference

@article{lebodicnemhauser2015,
title = "How important are branching decisions: Fooling \{MIP\} solvers ",
journal = "Operations Research Letters ",
volume = "43",
number = "3",
pages = "273 - 278",
year = "2015",
note = "",
issn = "0167-6377",
doi = "http://dx.doi.org/10.1016/j.orl.2015.03.003",
url = "//www.sciencedirect.com/science/article/pii/S0167637715000413",
author = "Pierre Le Bodic and George L. Nemhauser",
keywords = "Mixed integer programming solvers",
keywords = "Branch and bound",
keywords = "Tree size",
keywords = "Edge coloring",
keywords = "Chromatic index "
}