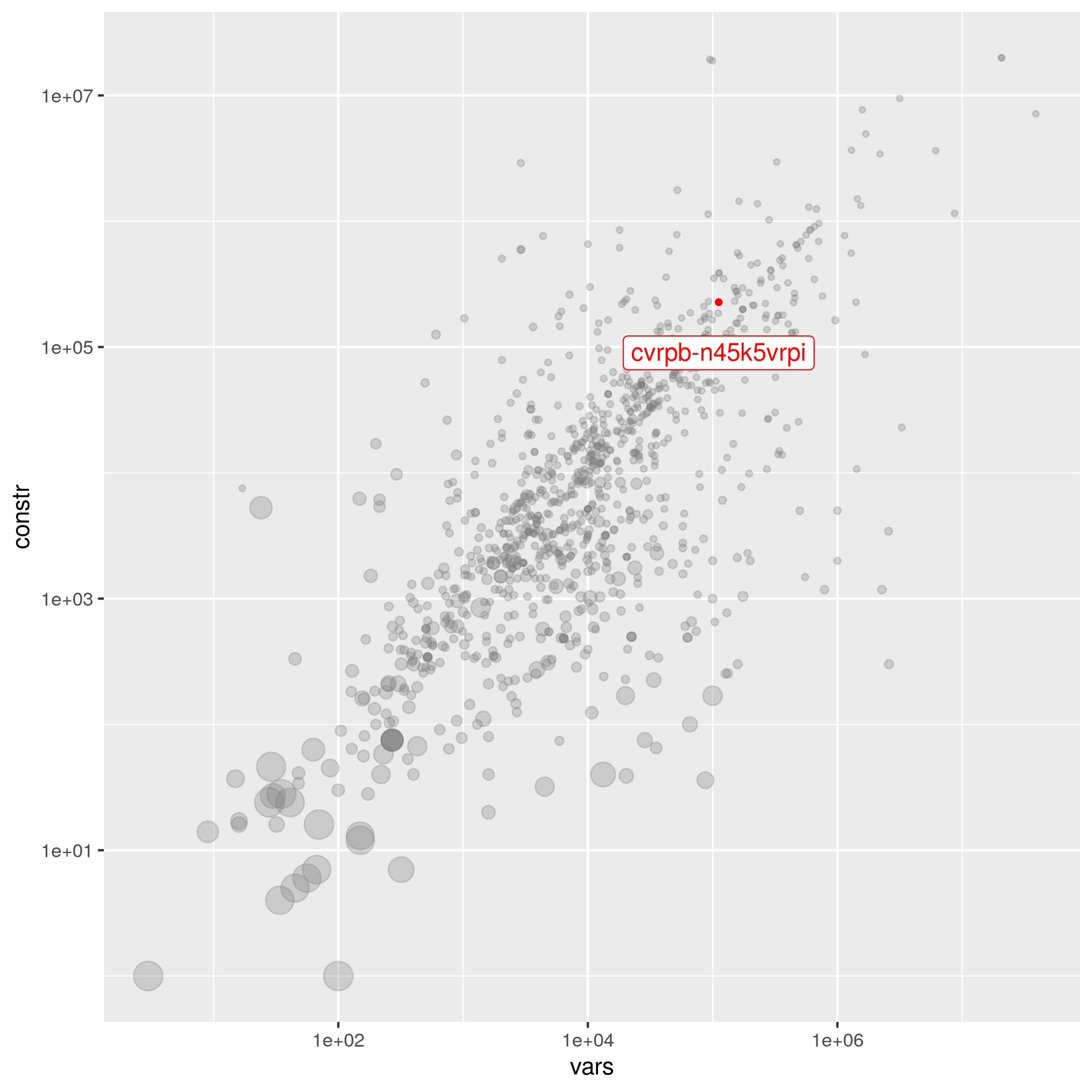
cvrpb-n45k5vrpi
indicator numerics aggregations precedence variable_bound set_partitioning set_packing mixed_binary general_linear
| Submitter | Variables | Constraints | Density | Status | Group | Objective | MPS File |
|---|---|---|---|---|---|---|---|
| Gleb Belov | 153202 | 268835 | 1.26149e-05 | open | pb- | 775* | cvrpb-n45k5vrpi.mps.gz |
These are the instances from MiniZinc Challenges 2012-2016 (see www.minizinc.org), compiled for MIP WITH INDICATOR CONSTRAINTS using the develop branch of MiniZinc and CPLEX 12.7.1 on 30 April 2017. Thus, these instances can only be handled by solvers accepting indicator constraints. For instances compiled with big-M/domain decomposition only, see my previous submission to MIPLIB. To recompile, create a directory MODELS, a list lst12_16.txt of the instances with full paths to mzn/dzn files of each instance per line, and say $> ~/install/libmzn/tests/benchmarking/mzn-test.py -l ../lst12_16.txt –slvPrf MZN-CPLEX –debug 1 –addOption “–timeout 3 -D fIndConstr=true -D fMIPdomains=false” –useJoinedName “–writeModel MODELS_IND/%s.mps” Alternatively, you can compile individual instance as follows: $> mzn-cplex -v -s -G linear –output-time ../challenge_2012_2016/mznc2016_probs/zephyrus/zephyrus.mzn ../challenge_2012_2016/mznc2016_p/zephyrus/14__8__6__3.dzn -a –timeout 3 -D fIndConstr=true -D fMIPdomains=false –writeModel MODELS_IND/challenge_2012_2016mznc2016_probszephyruszephyrusmzn-challenge_2012_2016mznc2016_probszephyrus14__8__6__3dzn.mps
Instance Statistics
Detailed explanation of the following tables can be found here.
| Original | Presolved | |
|---|---|---|
| Variables | 153202 | 111837 |
| Constraints | 268835 | 227166 |
| Binaries | 23625 | 15924 |
| Integers | 1575 | 1575 |
| Continuous | 128002 | 94338 |
| Implicit Integers | 348 | 524 |
| Fixed Variables | 308 | 0 |
| Nonzero Density | 1.26149e-05 | 1.25924e-05 |
| Nonzeroes | 519556 | 319916 |
| Original | Presolved | |
|---|---|---|
| Total | 153201 | 140884 |
| Empty | 0 | 0 |
| Free | 0 | 0 |
| Singleton | 572 | 19098 |
| Aggregations | 12798 | 8970 |
| Precedence | 480 | 32914 |
| Variable Bound | 696 | 33478 |
| Set Partitioning | 176 | 176 |
| Set Packing | 176 | 176 |
| Set Covering | 0 | 0 |
| Cardinality | 0 | 0 |
| Invariant Knapsack | 88 | 0 |
| Equation Knapsack | 0 | 0 |
| Bin Packing | 0 | 0 |
| Knapsack | 0 | 0 |
| Integer Knapsack | 0 | 0 |
| Mixed Binary | 115374 | 30712 |
| General Linear | 22841 | 15360 |
| Indicator | 115634 | 115634 |
Structure
Available nonzero structure and decomposition information. Further information can be found here.

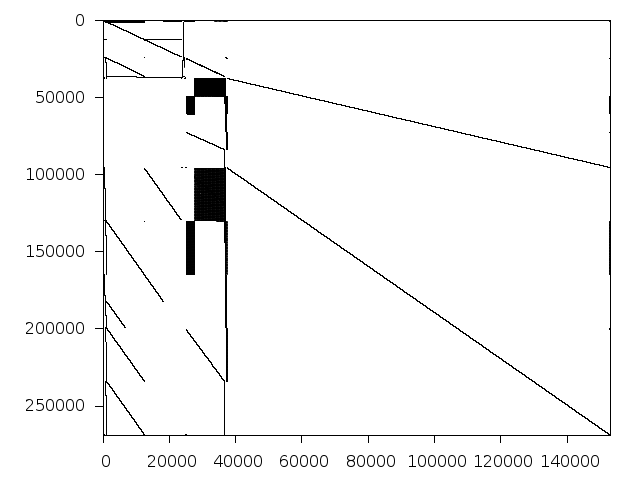
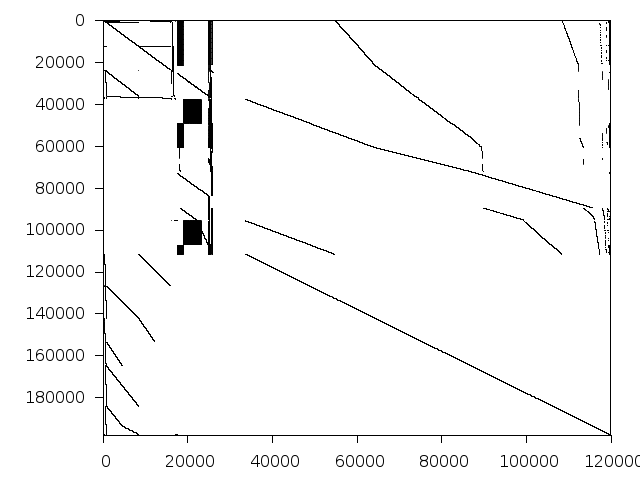
Decomposed structure of original problem (dec-file)
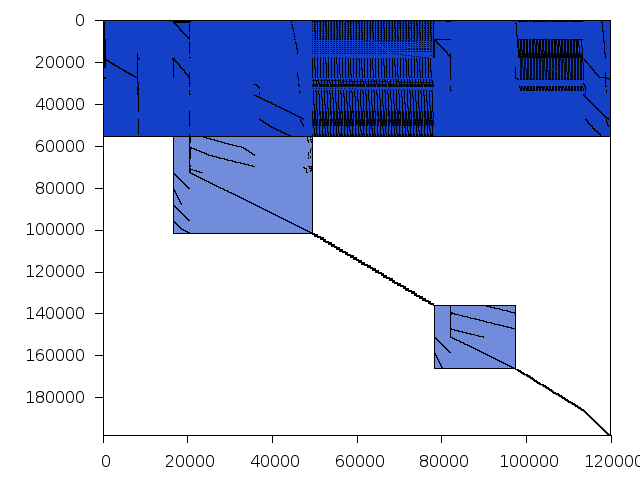
Decomposed structure after trivial presolving (dec-file)
| value | min | median | mean | max | |
|---|---|---|---|---|---|
| Components | |||||
| Constraint % | |||||
| Variable % | |||||
| Score |
Best Known Solution(s)
Find solutions below. Download the archive containing all solutions from the Download page.
## Warning in lapply(df["exactobjval"], as.numeric): NAs introduced by coercion| ID | Objective | Exact | Int. Viol | Cons. Viol | Obj. Viol | Submitter | Date | Description |
|---|---|---|---|---|---|---|---|---|
| 2 | 775 | 1e+100 | 0 | 0 | 0 | Frederic Didier | 2020-01-22 | Obtained with Google OR-tools using 8 Threads through generating subproblems by fixing part of the current solution and trying to solve them with a sub CP-SAT solver |
| 1 | 2009 | 0 | 0 | 0 | - | 2018-10-13 | Solution found during MIPLIB2017 problem selection. |
Similar instances in collection
The following instances are most similar to cvrpb-n45k5vrpi in the collection. This similarity analysis is based on 100 scaled instance features describing properties of the variables, objective function, bounds, constraints, and right hand sides.
Reference
@article{MZChPhil2010,
year={2010},
journal={Constraints},
volume={15},
number={3},
title={Philosophy of the {MiniZinc} challenge},
publisher={Springer US},
author={Stuckey, P. J. and Becket, R. and Fischer, J.},
pages={307--316},
}
@incollection{BelovEtAl_Lin16,
author="Belov, G.
and Stuckey, P. J.
and Tack, G.
and Wallace, M.",
editor="Rueher, M.",
title="Improved Linearization of Constraint Programming Models",
bookTitle="Principles and Practice of Constraint Programming: 22nd International Conference, CP 2016, Proceedings",
year="2016",
publisher="Springer International Publishing",
pages="49--65",
}Last Update 2024 by Julian Manns
generated with R Markdown
© by Zuse Institute Berlin (ZIB)
Imprint