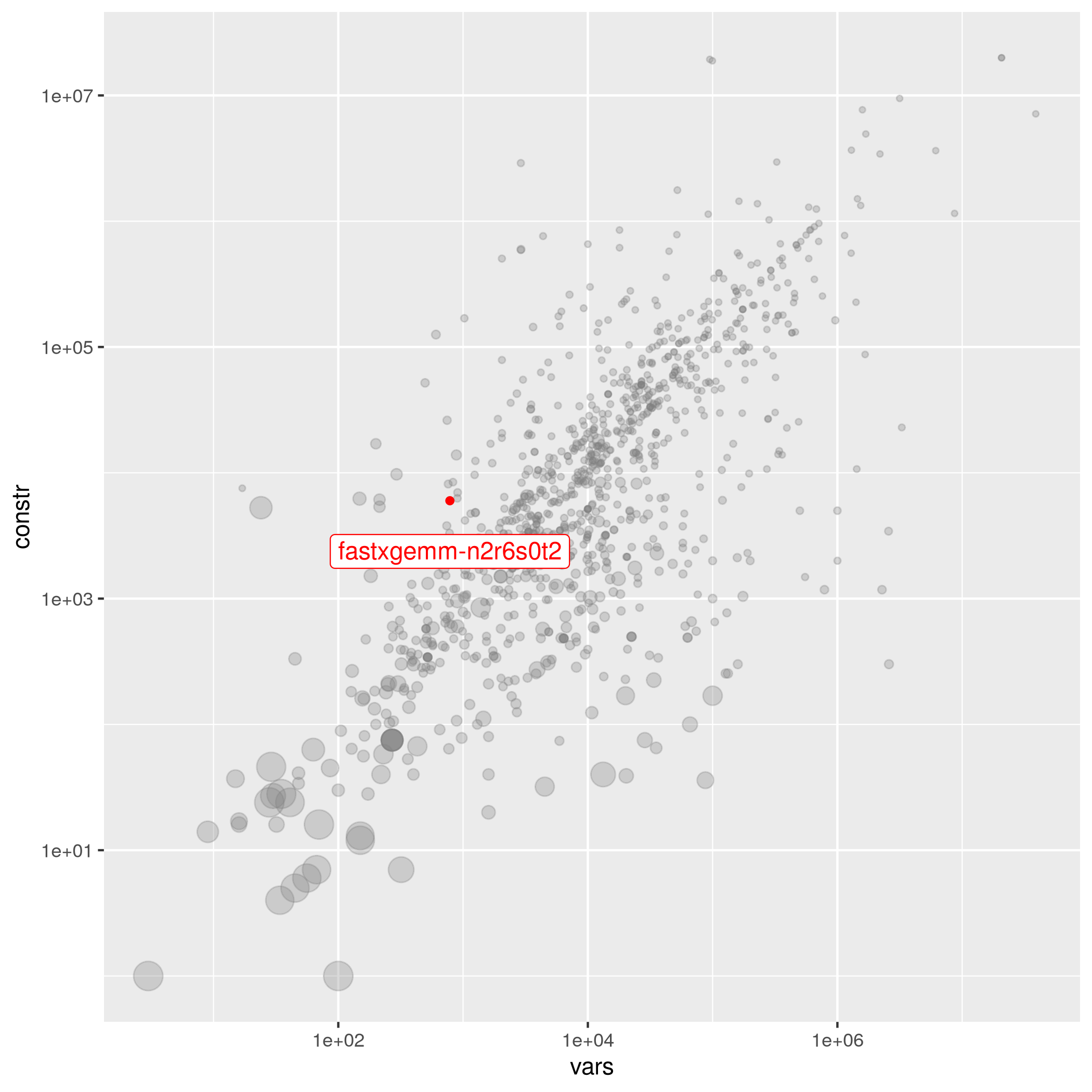
fastxgemm-n2r6s0t2

benchmark decomposition benchmark_suitable variable_bound set_partitioning set_covering mixed_binary general_linear

Submitter	Variables	Constraints	Density	Status	Group	Objective	MPS File
Laurent Sorber	784	5998	4.12042e-03	easy	fastxgemm	230	fastxgemm-n2r6s0t2.mps.gz

Naive multiplication of two N by N matrices requires N^3 scalar multiplications. For N=2, Strassen showed that it could be done in only R=7 < 8=N^3 multiplications. For N=3, it is known that 19 <= R <= 23, and for N=4 it is known that 34 <= R <= 49. This repository contains code that generates a mixed-integer linear program (MILP) formulation of the fast matrix multiplication problem for finding solutions with R < N^3 and proving that they are optimal. For a more detailed description, see the accompanying manuscript.

Location of instance in collection

Instance Statistics

Detailed explanation of the following tables can be found here.

Size Related Properties
	Original	Presolved
Variables	784	784
Constraints	5998	5998
Binaries	48	48
Integers	0	144
Continuous	736	592
Implicit Integers	0	144
Fixed Variables	0	0
Nonzero Density	0.00412042	0.00412042
Nonzeroes	19376	19376

Constraint Classification Properties
	Original	Presolved
Total	5998	5998
Empty	0	0
Free	0	0
Singleton	0	0
Aggregations	0	0
Precedence	1224	0
Variable Bound	1224	2448
Set Partitioning	0	72
Set Packing	0	0
Set Covering	0	30
Cardinality	0	0
Invariant Knapsack	0	0
Equation Knapsack	0	0
Bin Packing	0	0
Knapsack	0	0
Integer Knapsack	0	0
Mixed Binary	3550	304
General Linear	0	3144
Indicator	0	0

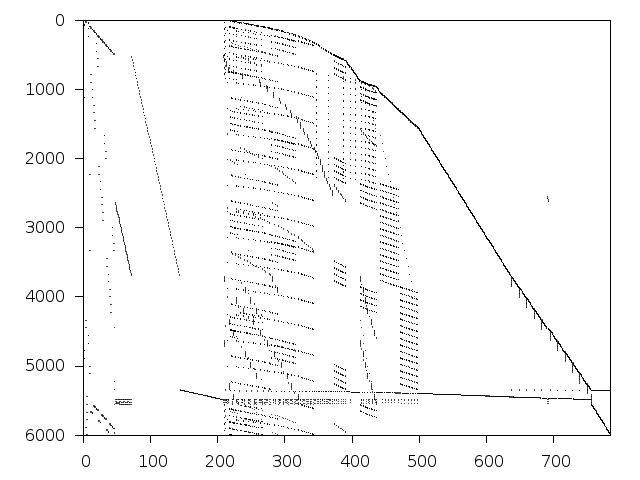
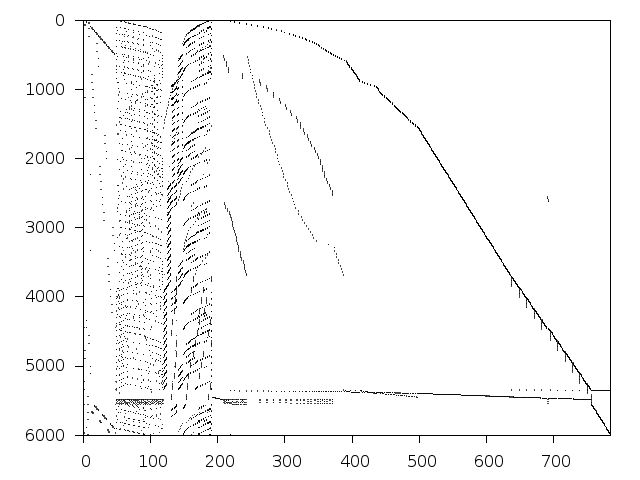
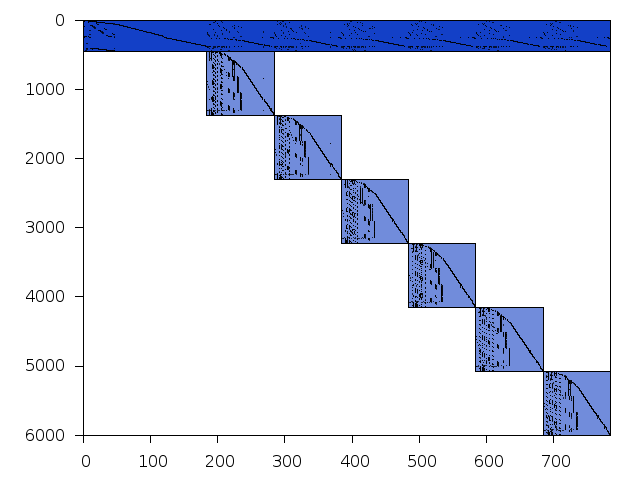
Structure

Available nonzero structure and decomposition information. Further information can be found here.

Nonzero entries of original problem

Nonzero entries after trivial presolving

Decomposed structure of original problem (dec-file)

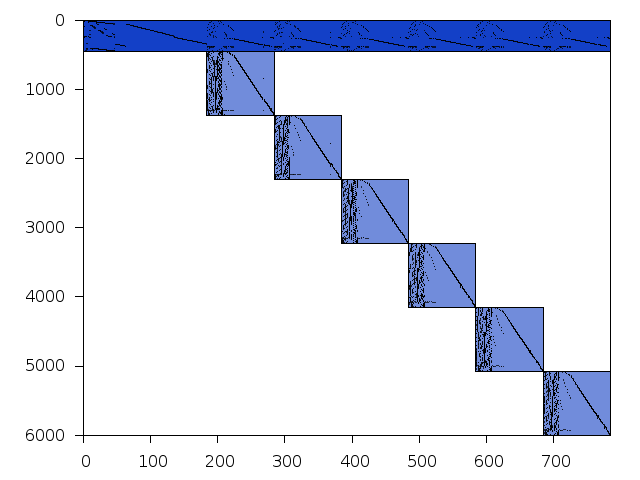
Decomposed structure after trivial presolving (dec-file)

	value	min	median	mean	max
Components	0.845098
Constraint %		15.4385	15.4385	15.4385	15.4385
Variable %		12.7551	12.7551	12.7551	12.7551
Score	0.808157

Best Known Solution(s)

Find solutions below. Download the archive containing all solutions from the Download page.

ID	Objective	Exact	Int. Viol	Cons. Viol	Obj. Viol	Submitter	Date	Description
1	230	230	0	0	0	-	2018-10-13	Solution found during MIPLIB2017 problem selection.

Similar instances in collection

The following instances are most similar to fastxgemm-n2r6s0t2 in the collection. This similarity analysis is based on 100 scaled instance features describing properties of the variables, objective function, bounds, constraints, and right hand sides.

Instance	Status	Variables	Binaries	Integers	Continuous	Constraints	Nonz.	Submitter	Group	Objective	Tags
fastxgemm-n2r7s4t1	easy	904	56	0	848	6972	22584	Laurent Sorber	fastxgemm	41.99999999999998	decomposition benchmark_suitable variable_bound set_partitioning set_covering mixed_binary general_linear
fastxgemm-n3r21s3t6	open	18684	378	0	18306	219368	718146	Laurent Sorber	fastxgemm	4110.99800117485*	decomposition variable_bound set_partitioning set_covering mixed_binary general_linear
fastxgemm-n3r22s4t6	open	19539	396	0	19143	229742	752274	Laurent Sorber	fastxgemm	3101.998498499999*	decomposition variable_bound set_partitioning set_covering mixed_binary general_linear
fastxgemm-n3r23s5t6	open	20394	414	0	19980	240116	786402	Laurent Sorber	fastxgemm	3089.997998*	decomposition variable_bound set_partitioning set_covering mixed_binary general_linear
neos-4335793-snake	hard	30827	20473	7865	2489	37166	129119	Jeff Linderoth	neos-pseudoapplication-44	27	numerics aggregations precedence variable_bound set_packing cardinality invariant_knapsack knapsack mixed_binary general_linear

Reference

@misc{Sorber2017,
author = {Laurent Sorber and Marc Van Barel},
title = {{A mixed-integer linear program formulation for fast matrix multiplication}},
howpublished = "\url{https://github.com/lsorber/fast-matrix-multiplication/blob/master/latex/fast-matrix-multiplication.pdf}",
day = {30},
month = {April},
year = {2017}, 
note = "[Online]"
}