fhnw-sq3

infeasible feasibility precedence set_partitioning integer_knapsack general_linear

Submitter	Variables	Constraints	Density	Status	Group	Objective	MPS File
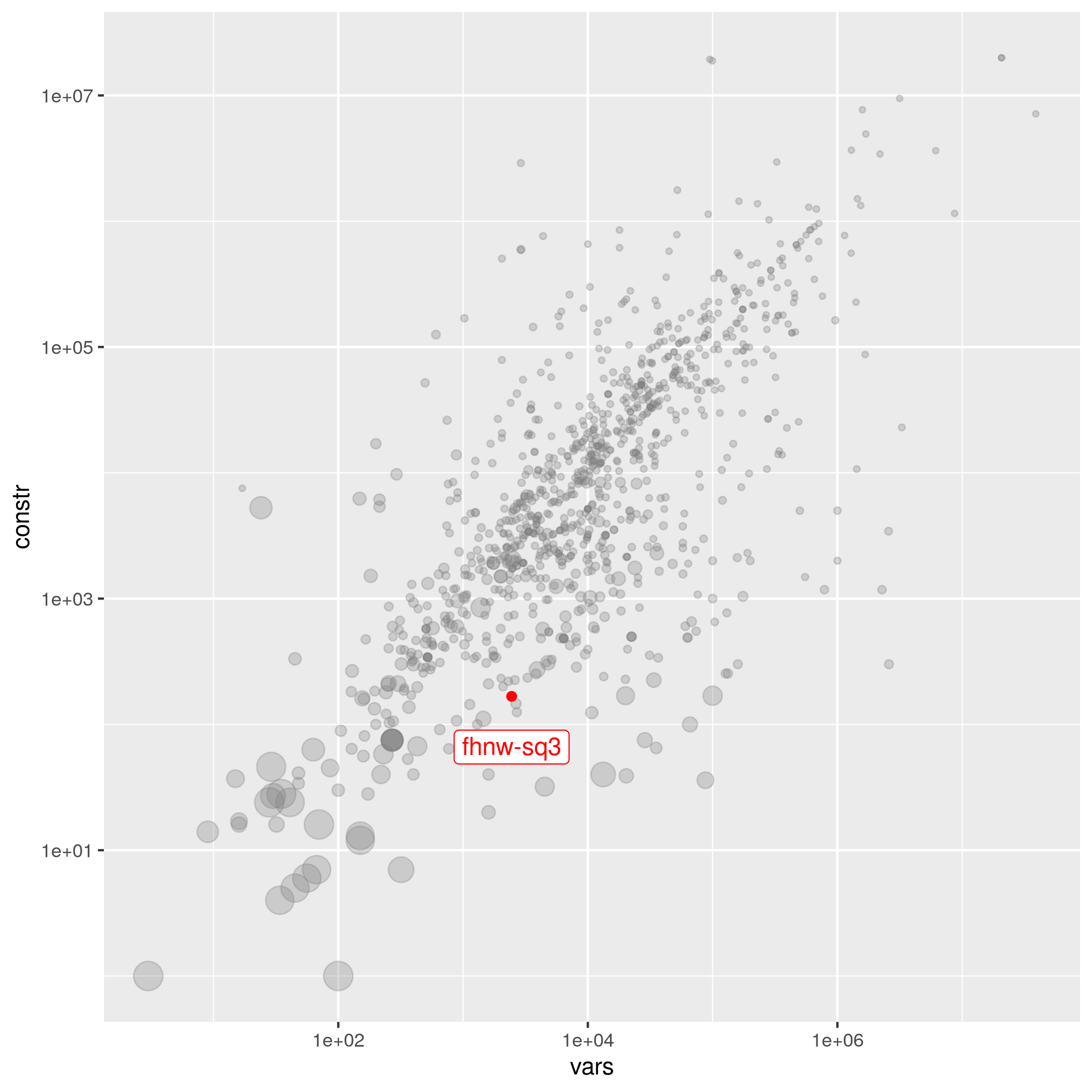
Simon Felix	2450	167	1.80178e-02	hard	fhnw-sq	Infeasible	fhnw-sq3.mps.gz

Combinatorial toy feasibility problem: Magic square. This instance is hard for all MIP solvers, but can be solved by customized codes. Infact, infeasibility can be deduced from a look at the model as explained by Ed Klotz: “But the easiest way is just by looking at the model itself. It’s a magic square problem with a few side constraints. Just remove the side constraints, and for that matter you can even remove remove the constraints on the sums of the diagonals of the square. So you are left to fill in a 7x7 magic square where the row sums are an even number (1544). If you look at the 49 values to place in the square, exactly 2 of them are odd. Regardless of where you place them, you are guaranteed to have at least 2 rows or columns involving one odd and 6 even numbers. Those rows cannot possibly add up to an even number, so no feasible solution exists.””

Location of instance in collection

Instance Statistics

Detailed explanation of the following tables can be found here.

Size Related Properties
	Original	Presolved
Variables	2450	2450
Constraints	167	167
Binaries	2401	2401
Integers	49	49
Continuous	0	0
Implicit Integers	0	49
Fixed Variables	0	0
Nonzero Density	0.0180178	0.0180178
Nonzeroes	7372	7372

Constraint Classification Properties
	Original	Presolved
Total	183	183
Empty	0	0
Free	0	0
Singleton	0	0
Aggregations	0	0
Precedence	4	4
Variable Bound	0	0
Set Partitioning	98	98
Set Packing	0	0
Set Covering	0	0
Cardinality	0	0
Invariant Knapsack	0	0
Equation Knapsack	0	0
Bin Packing	0	0
Knapsack	0	0
Integer Knapsack	16	16
Mixed Binary	0	0
General Linear	65	65
Indicator	0	0

Structure

Available nonzero structure and decomposition information. Further information can be found here.

Nonzero entries of original problem

Nonzero entries after trivial presolving

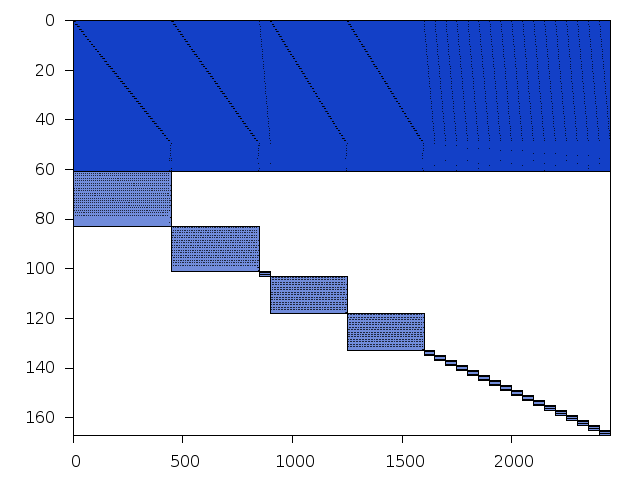
Decomposed structure of original problem (dec-file)

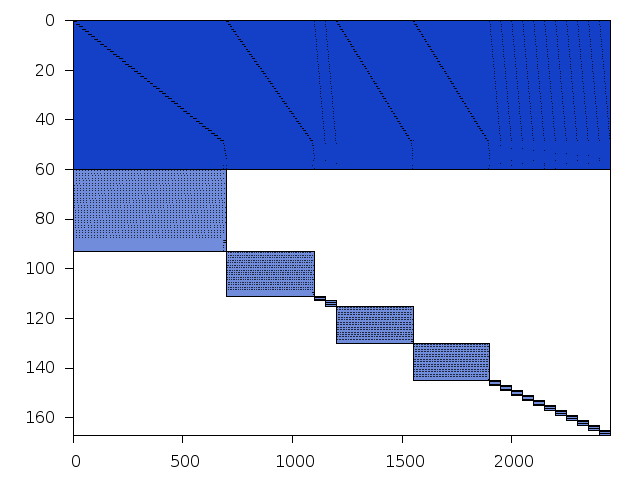
Decomposed structure after trivial presolving (dec-file)

	value	min	median	mean	max
Components	1.662758
Constraint %		0.598802	0.705256	0.598802	4.19162
Variable %		1.918370	2.088890	1.918370	7.67347
Score	0.308520

Best Known Solution(s)

No solution available for fhnw-sq3 .

Similar instances in collection

The following instances are most similar to fhnw-sq3 in the collection. This similarity analysis is based on 100 scaled instance features describing properties of the variables, objective function, bounds, constraints, and right hand sides.

Instance	Status	Variables	Binaries	Integers	Continuous	Constraints	Nonz.	Submitter	Group	Objective	Tags
fhnw-sq2	hard	650	625	25	0	91	1968	Simon Felix	fhnw-sq	0	feasibility precedence set_partitioning integer_knapsack general_linear
neos-5125849-lopori	easy	8130	8040	90	0	453	20938	Jeff Linderoth	neos-pseudoapplication-42	0	feasibility benchmark_suitable aggregations set_partitioning set_packing equation_knapsack general_linear
fiball	easy	34219	33960	258	1	3707	104792	MIPLIB submission pool	–	138	benchmark decomposition benchmark_suitable aggregations precedence set_partitioning general_linear
neos-3004026-krka	easy	17030	16900	130	0	12545	41860	Jeff Linderoth	neos-pseudoapplication-38	0	benchmark feasibility benchmark_suitable set_partitioning general_linear
neos-1354092	easy	13702	13282	420	0	3135	187187	NEOS Server Submission	neos-pseudoapplication-47	46	benchmark decomposition benchmark_suitable variable_bound set_partitioning general_linear

Reference

No bibliographic information available