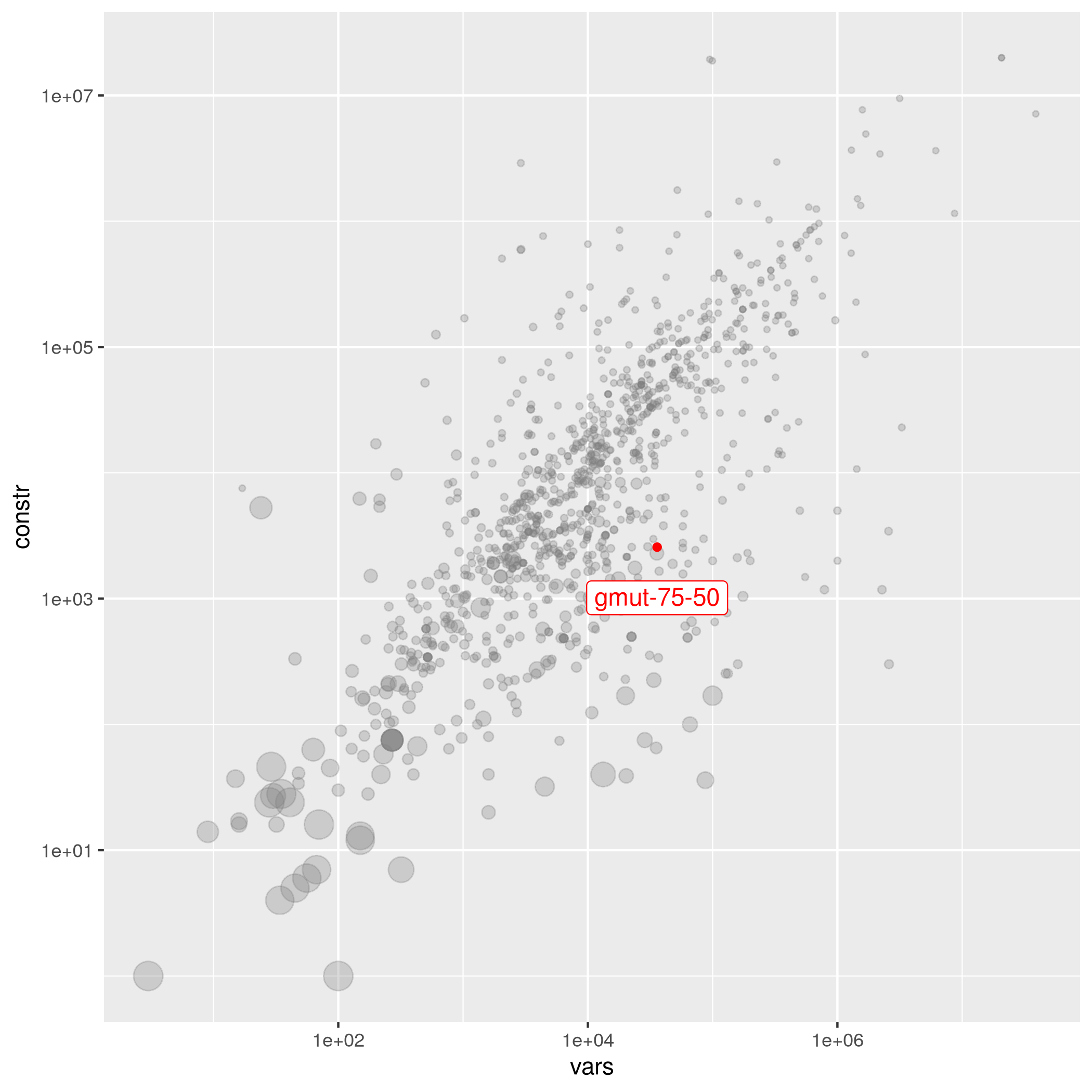
gmut-75-50
variable_bound set_packing mixed_binary
| Submitter | Variables | Constraints | Density | Status | Group | Objective | MPS File |
|---|---|---|---|---|---|---|---|
| Nora Konnyu | 68865 | 2565 | 3.23528e-03 | hard | gmu | -14180699.047 | gmut-75-50.mps.gz |
Timber harvest scheduling model. Solved by ParaXpress in a 12288 core supercomputer run on HLRN III. These are harvest scheduling models of hypothetical forest planning problems where net timber revenues are maximized over a planning horizon subject to four sets of constraints: 1. Each management unit can be harvested only once over the planning horizon, 2. Volume harvested in one planning period should not be less or more than some portion of that in the preceding period, 3. Area-weighted average age of the forest by the end of the plan should notbe less than a certain target age. 4. Clearcut size in any planning period has to be below a specific limit. Decision variable are management units and generalized management units (group of management units with a combined area not exceeding the limit on clearcut size) and can be either fully harvested or left untouched in any planning period, therefore there is a binary restriction on the decision variables. Imported from the MIPLIB2010 submissions.
Instance Statistics
Detailed explanation of the following tables can be found here.
| Original | Presolved | |
|---|---|---|
| Variables | 68865 | 35915 |
| Constraints | 2565 | 2565 |
| Binaries | 68859 | 35909 |
| Integers | 0 | 0 |
| Continuous | 6 | 6 |
| Implicit Integers | 0 | 0 |
| Fixed Variables | 0 | 0 |
| Nonzero Density | 0.00323528 | 0.00620076 |
| Nonzeroes | 571475 | 571226 |
| Original | Presolved | |
|---|---|---|
| Total | 2565 | 2565 |
| Empty | 0 | 0 |
| Free | 0 | 0 |
| Singleton | 0 | 0 |
| Aggregations | 0 | 0 |
| Precedence | 0 | 0 |
| Variable Bound | 18 | 18 |
| Set Partitioning | 0 | 0 |
| Set Packing | 2540 | 2540 |
| Set Covering | 0 | 0 |
| Cardinality | 0 | 0 |
| Invariant Knapsack | 0 | 0 |
| Equation Knapsack | 0 | 0 |
| Bin Packing | 0 | 0 |
| Knapsack | 0 | 0 |
| Integer Knapsack | 0 | 0 |
| Mixed Binary | 7 | 7 |
| General Linear | 0 | 0 |
| Indicator | 0 | 0 |
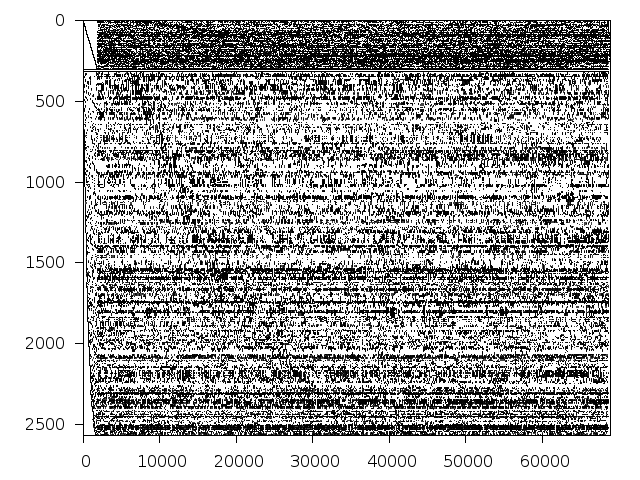
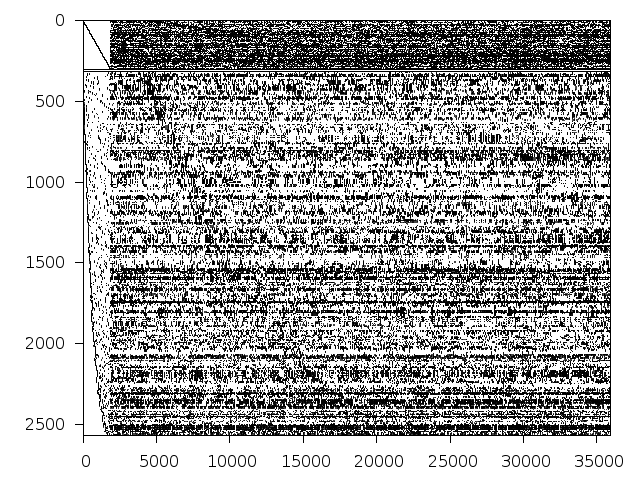
Structure
Available nonzero structure and decomposition information. Further information can be found here.

Decomposed structure of original problem (dec-file)
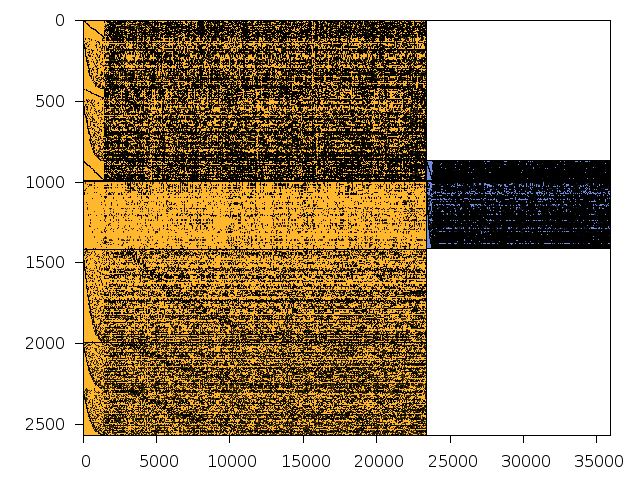
Decomposed structure after trivial presolving (dec-file)
| value | min | median | mean | max | |
|---|---|---|---|---|---|
| Components | 0.7781512 | ||||
| Constraint % | 0.0779727 | 0.140351 | 0.0779727 | 0.3898640 | |
| Variable % | 0.0055700 | 0.007800 | 0.0055700 | 0.0167061 | |
| Score | 0.0070170 |
Best Known Solution(s)
Find solutions below. Download the archive containing all solutions from the Download page.
| ID | Objective | Exact | Int. Viol | Cons. Viol | Obj. Viol | Submitter | Date | Description |
|---|---|---|---|---|---|---|---|---|
| 1 | -14180418 | -14180418 | 0 | 0 | 0 | - | 2018-10-12 | Solution found during MIPLIB2017 problem selection. |
Similar instances in collection
The following instances are most similar to gmut-75-50 in the collection. This similarity analysis is based on 100 scaled instance features describing properties of the variables, objective function, bounds, constraints, and right hand sides.
| Instance | Status | Variables | Binaries | Integers | Continuous | Constraints | Nonz. | Submitter | Group | Objective | Tags |
|---|---|---|---|---|---|---|---|---|---|---|---|
| gmut-76-50 | open | 68865 | 68859 | 0 | 6 | 2586 | 470045 | Nora Konnyu | gmu | -14171893.7789212* | variable_bound set_packing mixed_binary |
| gmut-76-40 | open | 24338 | 24332 | 0 | 6 | 2586 | 153017 | Nora Konnyu | gmu | -14169441.78* | variable_bound set_packing mixed_binary |
| gmu-35-50 | easy | 1919 | 1914 | 0 | 5 | 435 | 8643 | Nora Konnyu | gmu | -2607958.33 | benchmark benchmark_suitable variable_bound set_packing mixed_binary |
| gmu-35-40 | easy | 1205 | 1200 | 0 | 5 | 424 | 4843 | Nora Konnyu | gmu | -2406733.3688 | benchmark benchmark_suitable variable_bound set_packing mixed_binary |
| supportcase31 | open | 488882 | 488760 | 0 | 122 | 26195 | 1833861 | Domenico Salvagnin | – | -3720089.081* | decomposition numerics precedence set_packing invariant_knapsack knapsack mixed_binary |
Reference
No bibliographic information availableLast Update 2024 by Julian Manns
generated with R Markdown
© by Zuse Institute Berlin (ZIB)
Imprint