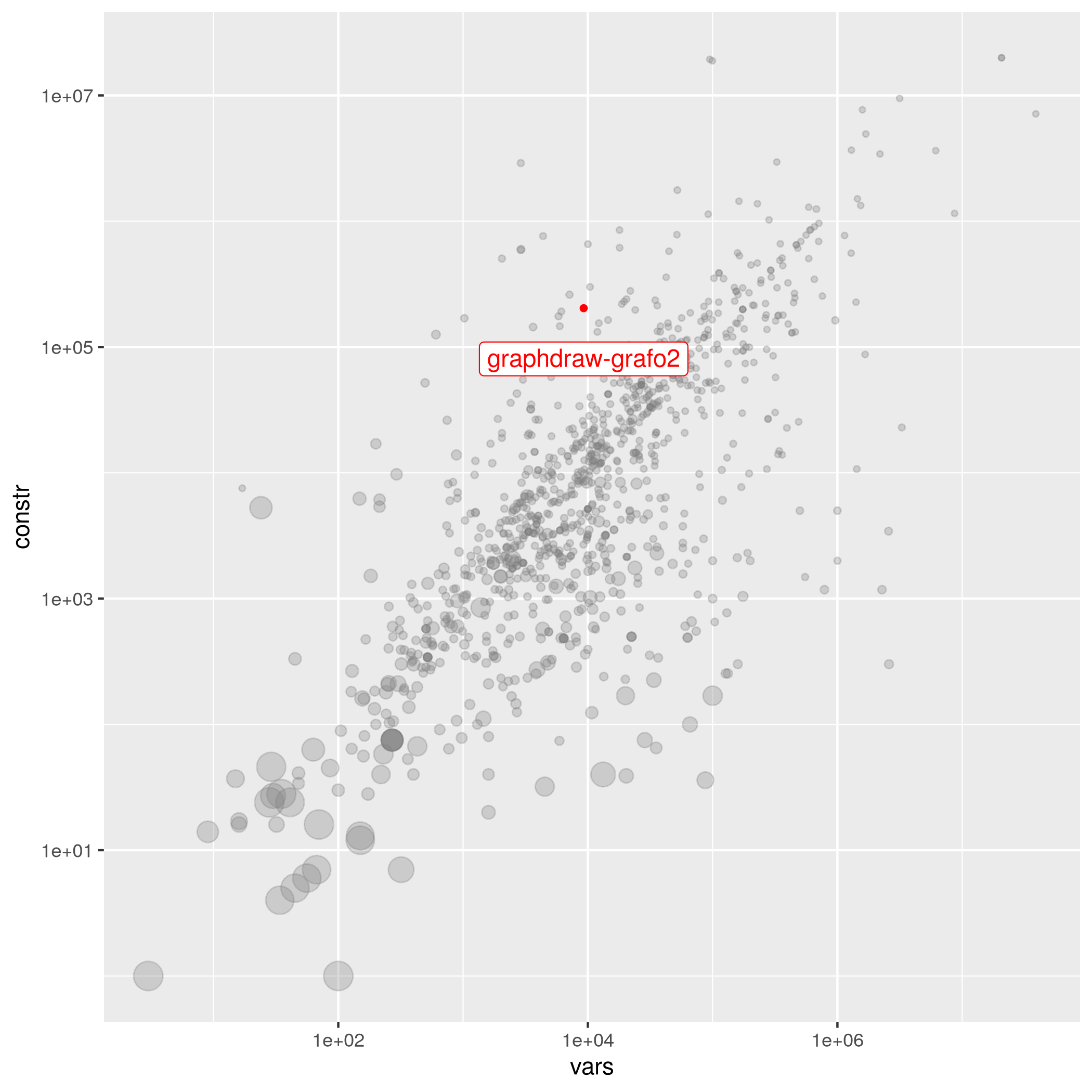
graphdraw-grafo2
variable_bound set_partitioning invariant_knapsack mixed_binary general_linear
| Submitter | Variables | Constraints | Density | Status | Group | Objective | MPS File |
|---|---|---|---|---|---|---|---|
| Cézar Augusto Nascimento e Silva | 9258 | 203455 | 3.25106e-04 | open | graphdraw | 72118.5* | graphdraw-grafo2.mps.gz |
In the Graph Drawing problem a set of symbols must be placed in a plane and their connections routed. The objective is to produce aesthetically pleasant, easy to read diagrams. As a primary concern one usually tries to minimize edges crossing, edges’ length, waste of space and number of bents in the connections. When formulated with these constraints the problem becomes NP-Hard . In practice many additional complicating requirements can be included, such as non-uniform sizes for symbols. Thus, some heuristics such as the generalized force-direct method and Simulated Annealing have been proposed to tackle this problem. uses a grid structure to approach the Entity-Relationship (ER) drawing problem, emphasizing the differences between ER drawing and the more classical circuit drawing problems. presented different ways of producing graph layouts (e.g.: tree, orthogonal, visibility representations, hierarchic, among others) for general graphs with applications on different subjects. The ability to automatically produce high quality layouts is very important in many applications, one of these is Software Engineering: the availability of easy to understand ER diagrams, for instance, can improve the time needed for developers to master database models and increase their productivity. Our solution approach involves two phases: (\(i\)) firstly the optimal placement of entities is solved, i.e.: entities are positioned so as to minimize the distances between connected entities; and (\(ii\)) secondly, edges are routed minimizing bends and avoiding the inclusion of connectors too close. We present the model for the first phase of our problem.
Instance Statistics
Detailed explanation of the following tables can be found here.
| Original | Presolved | |
|---|---|---|
| Variables | 9258 | 9258 |
| Constraints | 203455 | 203455 |
| Binaries | 8844 | 8844 |
| Integers | 134 | 134 |
| Continuous | 280 | 280 |
| Implicit Integers | 0 | 0 |
| Fixed Variables | 0 | 0 |
| Nonzero Density | 0.000325106 | 0.000325106 |
| Nonzeroes | 612366 | 612366 |
| Original | Presolved | |
|---|---|---|
| Total | 203455 | 203455 |
| Empty | 0 | 0 |
| Free | 0 | 0 |
| Singleton | 0 | 0 |
| Aggregations | 0 | 0 |
| Precedence | 0 | 0 |
| Variable Bound | 341 | 341 |
| Set Partitioning | 2211 | 2211 |
| Set Packing | 0 | 0 |
| Set Covering | 0 | 0 |
| Cardinality | 0 | 0 |
| Invariant Knapsack | 191620 | 191620 |
| Equation Knapsack | 0 | 0 |
| Bin Packing | 0 | 0 |
| Knapsack | 0 | 0 |
| Integer Knapsack | 0 | 0 |
| Mixed Binary | 147 | 147 |
| General Linear | 9136 | 9136 |
| Indicator | 0 | 0 |
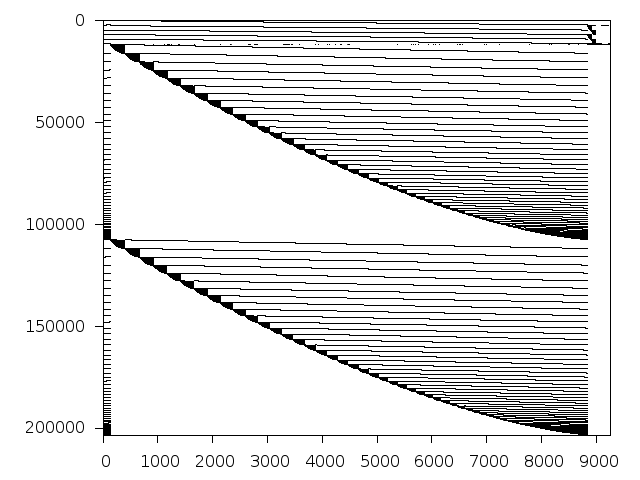
Structure
Available nonzero structure and decomposition information. Further information can be found here.
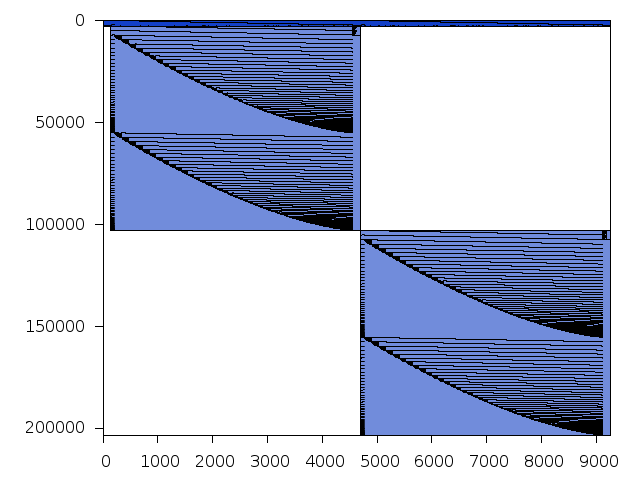
Decomposed structure of original problem (dec-file)
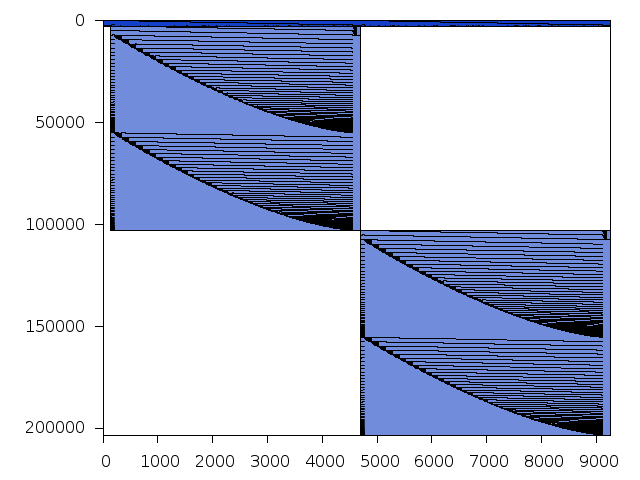
Decomposed structure after trivial presolving (dec-file)
| value | min | median | mean | max | |
|---|---|---|---|---|---|
| Components | 0.4771212 | ||||
| Constraint % | 49.3367 | 49.3367 | 49.3367 | 49.3367 | |
| Variable % | 49.2763 | 49.2763 | 49.2763 | 49.2763 | |
| Score | 0.5005080 |
Best Known Solution(s)
Find solutions below. Download the archive containing all solutions from the Download page.
## Warning in lapply(df["exactobjval"], as.numeric): NAs introduced by coercion| ID | Objective | Exact | Int. Viol | Cons. Viol | Obj. Viol | Submitter | Date | Description |
|---|---|---|---|---|---|---|---|---|
| 4 | 72118.5 | 72118.5 | 1e-07 | 1e-07 | 0 | Edward Rothberg | 2020-04-22 | Obtained with Gurobi 9.0 using the solution improvement heuristic |
| 3 | 73377.0 | 72616.5 | 0e+00 | 0e+00 | 0 | Frederic Didier | 2020-01-22 | Obtained with Google OR-tools using 8 Threads through generating subproblems by fixing part of the current solution and trying to solve them with a sub CP-SAT solver |
| 2 | 95024.5 | 0e+00 | 0e+00 | 0 | Robert Ashford and Alkis Vazacopoulus | 2019-12-18 | Found with ODH|CPLEX | |
| 1 | 230722.5 | 230722.5 | 0e+00 | 0e+00 | 0 | - | 2018-10-13 | Solution found during MIPLIB2017 problem selection. |
Similar instances in collection
The following instances are most similar to graphdraw-grafo2 in the collection. This similarity analysis is based on 100 scaled instance features describing properties of the variables, objective function, bounds, constraints, and right hand sides.
| Instance | Status | Variables | Binaries | Integers | Continuous | Constraints | Nonz. | Submitter | Group | Objective | Tags |
|---|---|---|---|---|---|---|---|---|---|---|---|
| graphdraw-opmanager | open | 4812 | 4512 | 96 | 204 | 75395 | 227160 | Cézar Augusto Nascimento e Silva | graphdraw | 103535.4999999998* | variable_bound set_partitioning invariant_knapsack mixed_binary general_linear |
| graphdraw-mainerd | open | 2050 | 1860 | 62 | 128 | 20661 | 62350 | Cézar Augusto Nascimento e Silva | graphdraw | 39852.99999999995* | variable_bound set_partitioning invariant_knapsack mixed_binary general_linear |
| neos-3402294-bobin | easy | 2904 | 2616 | 0 | 288 | 591076 | 2034888 | Jeff Linderoth | neos-pseudoapplication-71 | 0.06724999999999949 | benchmark benchmark_suitable precedence set_partitioning set_covering invariant_knapsack mixed_binary |
| graphdraw-domain | easy | 254 | 180 | 20 | 54 | 865 | 2600 | Cézar Augusto Nascimento e Silva | graphdraw | 19685.99997550038 | benchmark benchmark_suitable variable_bound set_partitioning invariant_knapsack mixed_binary general_linear |
| neos-3695882-vesdre | open | 6135 | 5955 | 0 | 180 | 191504 | 598115 | Hans Mittelmann | neos-pseudoapplication-71 | 518.3505480226543* | decomposition variable_bound set_partitioning cardinality invariant_knapsack knapsack mixed_binary |
Reference
@article{ESILVA2017207,
title = {Drawing graphs with mathematical programming and variable neighborhood search},
journal = {Electronic Notes in Discrete Mathematics},
volume = {58},
pages = {207--214},
year = {2017},
issn = {1571-0653},
doi = {http://dx.doi.org/10.1016/j.endm.2017.03.027},
author = {Cézar Augusto N. e Silva and Haroldo Gambini Santos}
}Last Update 2024 by Julian Manns
generated with R Markdown
© by Zuse Institute Berlin (ZIB)
Imprint