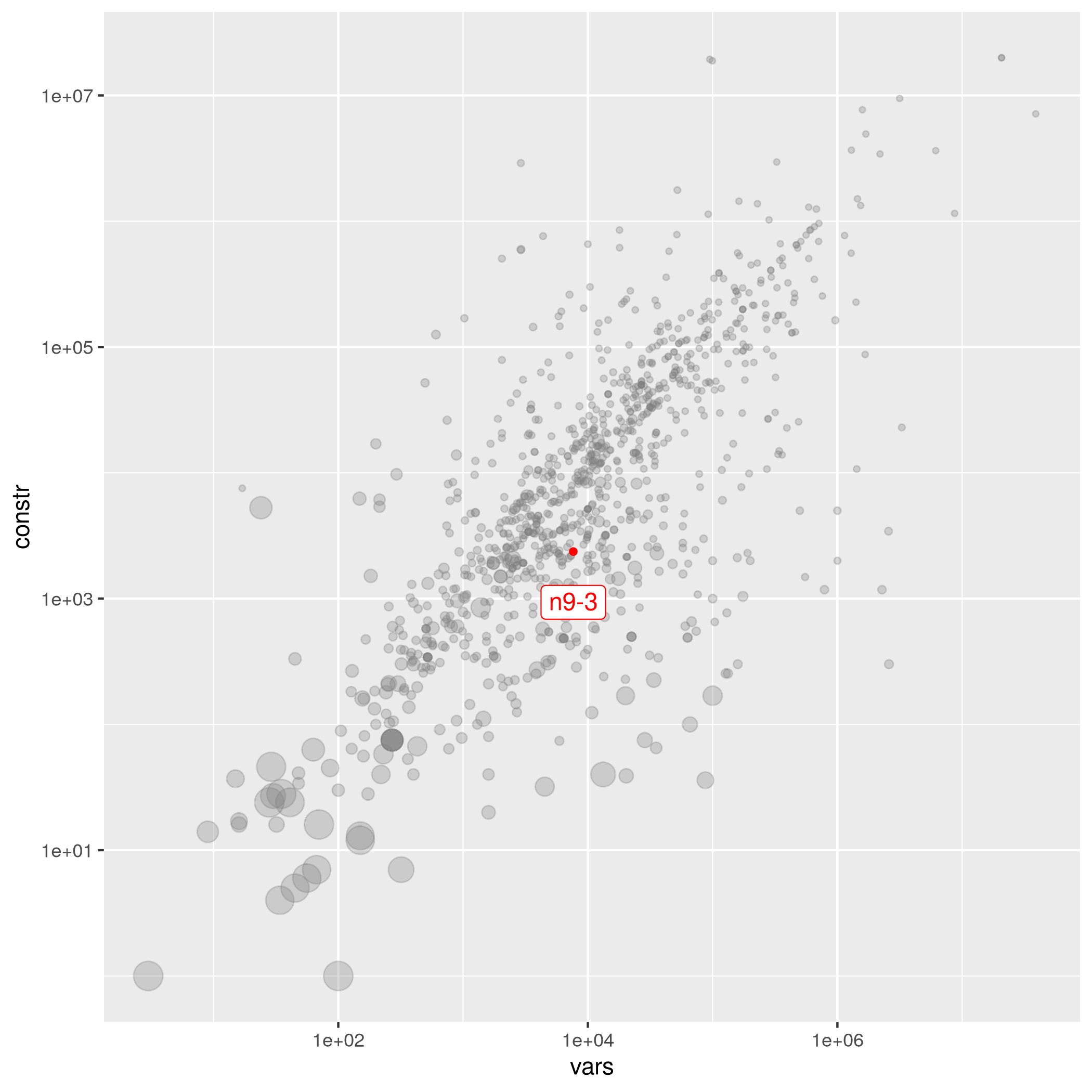
n9-3

decomposition benchmark_suitable aggregations mixed_binary general_linear

Submitter	Variables	Constraints	Density	Status	Group	Objective	MPS File
A. Atamtürk	7644	2364	1.66416e-03	easy	nxy-z	14409	n9-3.mps.gz

Capacitated network design problem Imported from MIPLIB2010.

Location of instance in collection

Instance Statistics

Detailed explanation of the following tables can be found here.

Size Related Properties
	Original	Presolved
Variables	7644	7644
Constraints	2364	2364
Binaries	0	0
Integers	252	252
Continuous	7392	7392
Implicit Integers	0	0
Fixed Variables	0	0
Nonzero Density	0.00166416	0.00166416
Nonzeroes	30072	30072

Constraint Classification Properties
	Original	Presolved
Total	2364	2364
Empty	0	0
Free	0	0
Singleton	0	0
Aggregations	176	176
Precedence	0	0
Variable Bound	0	0
Set Partitioning	0	0
Set Packing	0	0
Set Covering	0	0
Cardinality	0	0
Invariant Knapsack	0	0
Equation Knapsack	0	0
Bin Packing	0	0
Knapsack	0	0
Integer Knapsack	0	0
Mixed Binary	2020	2020
General Linear	168	168
Indicator	0	0

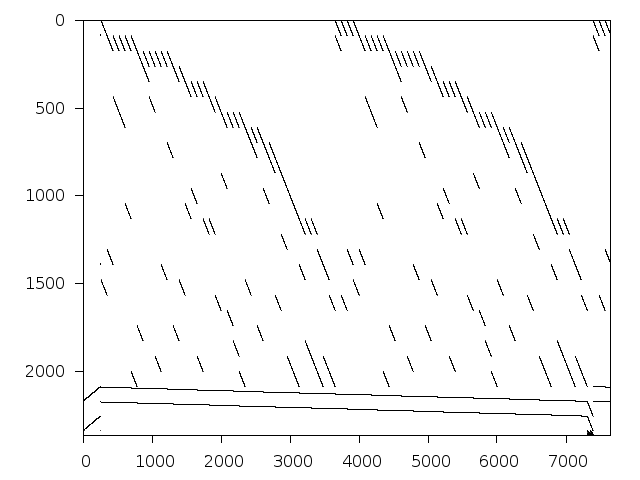
Structure

Available nonzero structure and decomposition information. Further information can be found here.

Nonzero entries of original problem

Nonzero entries after trivial presolving

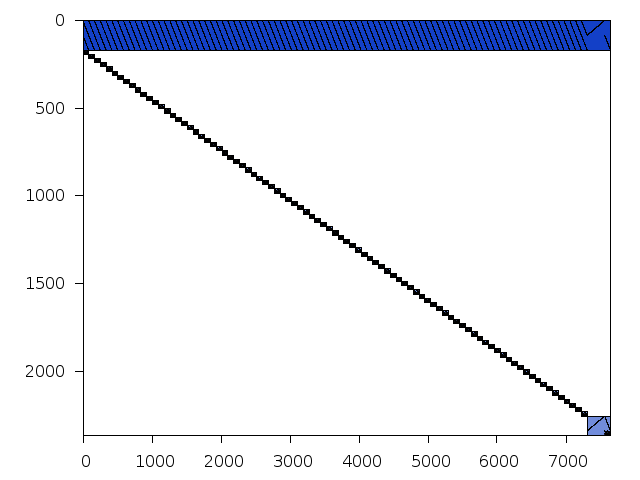
Decomposed structure of original problem (dec-file)

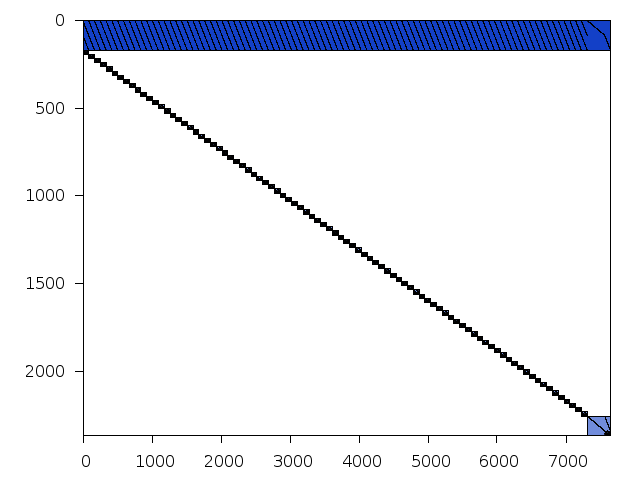
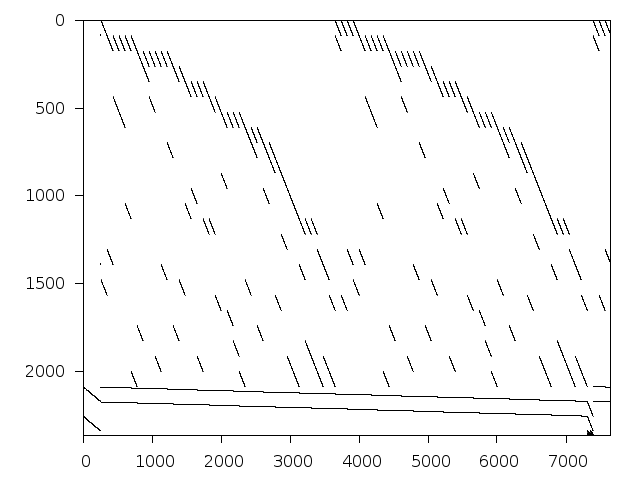
Decomposed structure after trivial presolving (dec-file)

	value	min	median	mean	max
Components	1.94939
Constraint %		1.01523	1.05561	1.01523	4.56853
Variable %		1.09890	1.13636	1.09890	4.39560
Score	0.91722

Best Known Solution(s)

Find solutions below. Download the archive containing all solutions from the Download page.

ID	Objective	Exact	Int. Viol	Cons. Viol	Obj. Viol	Submitter	Date	Description
2	14409	14409	0	0	0	-	2018-10-13	Solution imported from MIPLIB2010.
1	14409	14409	0	0	0	-	2018-10-13	Solution found during MIPLIB2017 problem selection.

Similar instances in collection

The following instances are most similar to n9-3 in the collection. This similarity analysis is based on 100 scaled instance features describing properties of the variables, objective function, bounds, constraints, and right hand sides.

Instance	Status	Variables	Integers	Continuous	Constraints	Nonz.	Submitter	Group	Objective	Tags
n6-3	easy	7178	222	6956	2760	28268	A. Atamtürk	nxy-z	15174.999303	decomposition benchmark_suitable aggregations mixed_binary general_linear
n5-3	easy	2550	150	2400	1062	9900	A. Atamtürk	nxy-z	8104.999999993999	benchmark decomposition benchmark_suitable aggregations mixed_binary general_linear
n7-3	easy	5626	174	5452	2336	22156	A. Atamtürk	nxy-z	15425.99999997	decomposition benchmark_suitable aggregations mixed_binary general_linear
n13-3	easy	3472	186	3286	1723	13516	A. Atamtürk	nxy-z	13385	decomposition benchmark_suitable aggregations mixed_binary general_linear
ger50-17-ptp-pop-3t	open	4892	540	4352	545	14285	C. Raack	ger50	5224.5144*	mixed_binary general_linear

Reference

@article{Atamturk2002,
 author = {A. Atamt{\"u}rk},
 journal = {Mathematical Programming},
 pages = {425--437},
 title = {On Capacitated Network Design Cut-Set Polyhedra},
 volume = {92},
 year = {2002}
}

@misc{bcol,
 key = {zzz bcol},
 note = {http://ieor.berkeley.edu/~atamturk/data/},
 title = {{B}erkeley {C}omputational {O}ptimization {L}ab -- {D}ata
{S}ets},
 year = {2010}
}