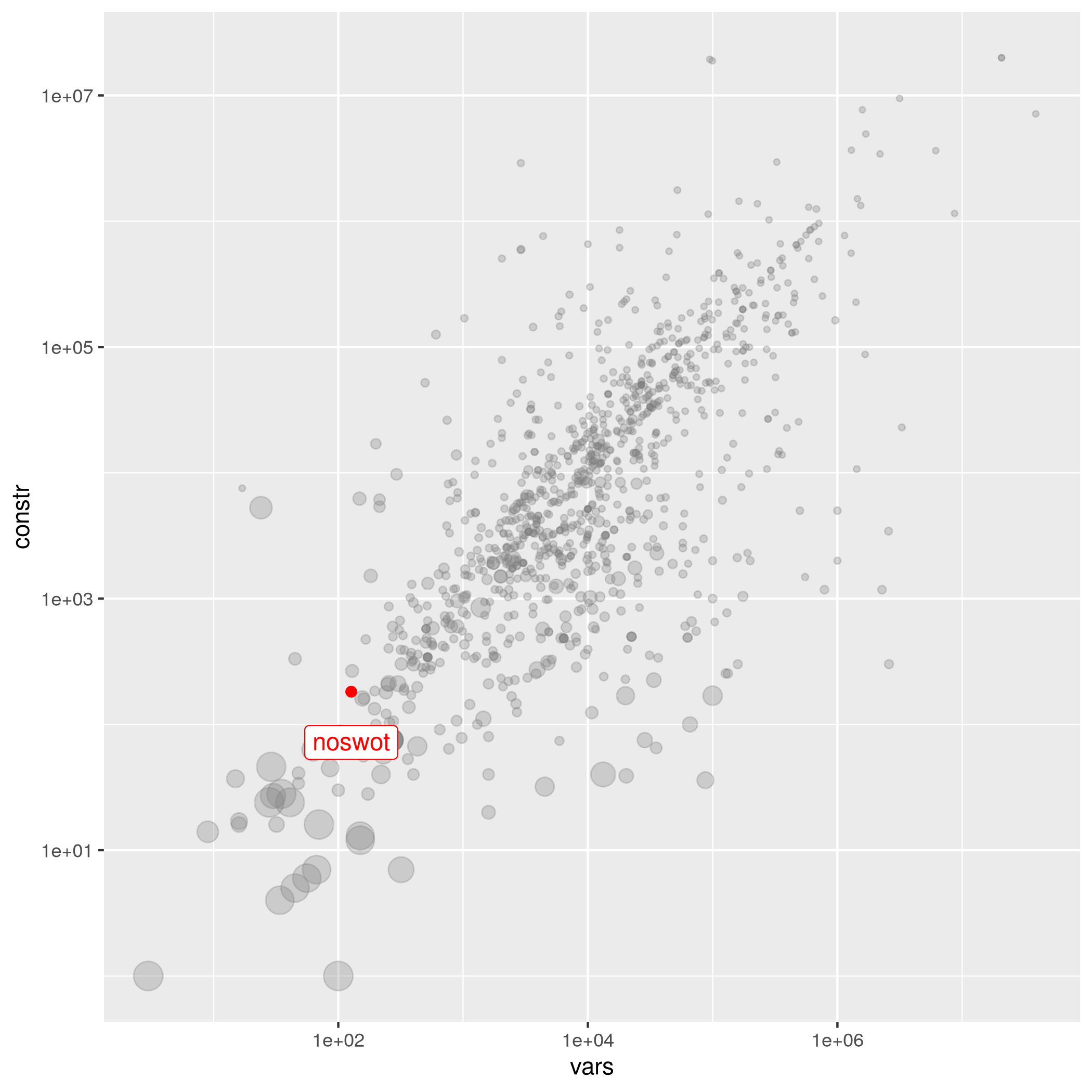
noswot
benchmark_suitable precedence variable_bound set_packing integer_knapsack mixed_binary general_linear
| Submitter | Variables | Constraints | Density | Status | Group | Objective | MPS File |
|---|---|---|---|---|---|---|---|
| J. Gregory, L. Schrage | 128 | 182 | 3.15505e-02 | easy | – | -41.00000885 | noswot.mps.gz |
Unknown application Imported from MIPLIB2010.
Instance Statistics
Detailed explanation of the following tables can be found here.
| Original | Presolved | |
|---|---|---|
| Variables | 128 | 127 |
| Constraints | 182 | 182 |
| Binaries | 75 | 80 |
| Integers | 25 | 20 |
| Continuous | 28 | 27 |
| Implicit Integers | 0 | 0 |
| Fixed Variables | 0 | 0 |
| Nonzero Density | 0.0315505 | 0.0316691 |
| Nonzeroes | 735 | 732 |
| Original | Presolved | |
|---|---|---|
| Total | 182 | 182 |
| Empty | 0 | 0 |
| Free | 0 | 0 |
| Singleton | 0 | 0 |
| Aggregations | 0 | 0 |
| Precedence | 0 | 8 |
| Variable Bound | 45 | 40 |
| Set Partitioning | 0 | 0 |
| Set Packing | 0 | 1 |
| Set Covering | 0 | 0 |
| Cardinality | 0 | 0 |
| Invariant Knapsack | 0 | 0 |
| Equation Knapsack | 0 | 0 |
| Bin Packing | 0 | 0 |
| Knapsack | 0 | 0 |
| Integer Knapsack | 6 | 5 |
| Mixed Binary | 0 | 27 |
| General Linear | 131 | 101 |
| Indicator | 0 | 0 |
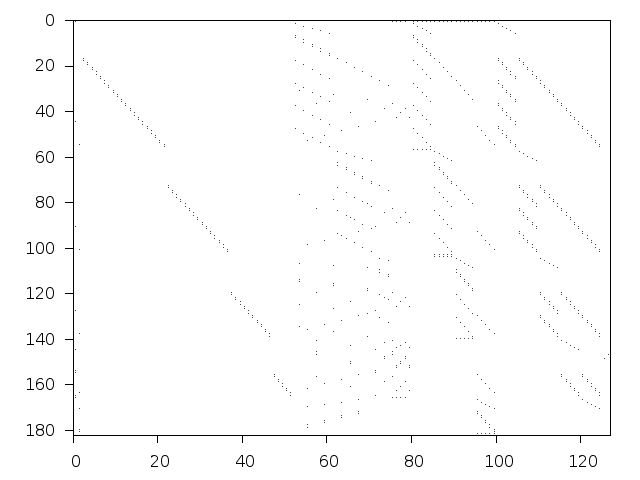
Structure
Available nonzero structure and decomposition information. Further information can be found here.
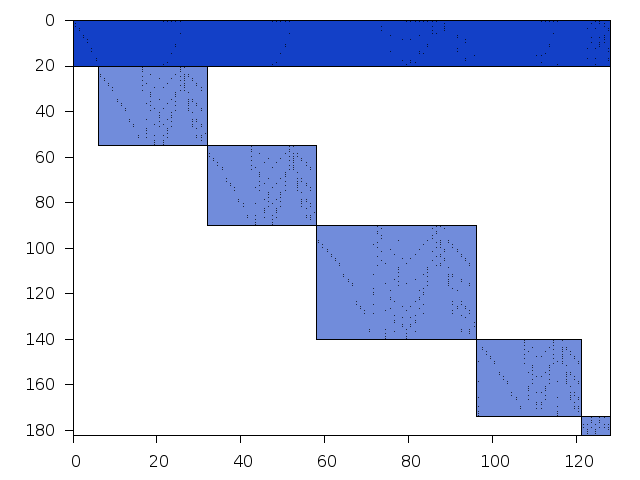
Decomposed structure of original problem (dec-file)
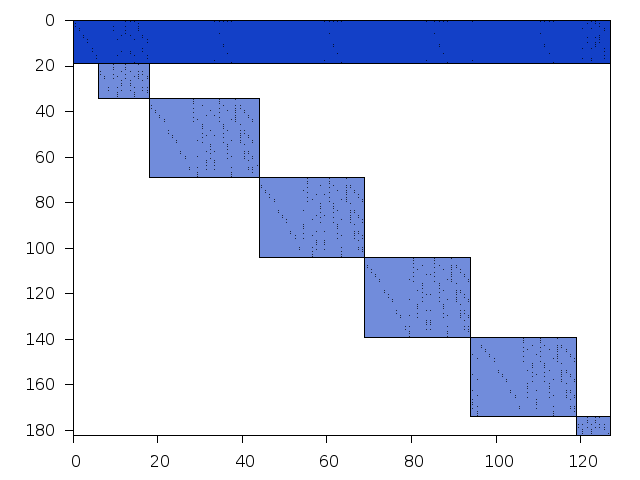
Decomposed structure after trivial presolving (dec-file)
| value | min | median | mean | max | |
|---|---|---|---|---|---|
| Components | 1.414973 | ||||
| Constraint % | 1.64835 | 1.64835 | 1.64835 | 1.64835 | |
| Variable % | 2.36220 | 2.42520 | 2.36220 | 3.14961 | |
| Score | 0.402094 |
Best Known Solution(s)
Find solutions below. Download the archive containing all solutions from the Download page.
| ID | Objective | Exact | Int. Viol | Cons. Viol | Obj. Viol | Submitter | Date | Description |
|---|---|---|---|---|---|---|---|---|
| 2 | -41.00000 | -41 | 0.0e+00 | 0 | 0 | - | 2018-10-10 | Solution imported from MIPLIB2010. |
| 1 | -41.00001 | -41 | 8.9e-06 | 0 | 0 | - | 2018-10-10 | Solution found during MIPLIB2017 problem selection. |
Similar instances in collection
The following instances are most similar to noswot in the collection. This similarity analysis is based on 100 scaled instance features describing properties of the variables, objective function, bounds, constraints, and right hand sides.
| Instance | Status | Variables | Binaries | Integers | Continuous | Constraints | Nonz. | Submitter | Group | Objective | Tags |
|---|---|---|---|---|---|---|---|---|---|---|---|
| milo-v12-6-r2-40-1 | easy | 2688 | 840 | 0 | 1848 | 5628 | 14604 | Tamas Terlaky | milo | 326481.14282799 | benchmark decomposition benchmark_suitable aggregations precedence variable_bound mixed_binary general_linear |
| milo-v13-4-3d-3-0 | hard | 516 | 120 | 0 | 396 | 996 | 2456 | Tamas Terlaky | milo | 273238.08563337 | aggregations variable_bound mixed_binary general_linear |
| milo-v13-4-3d-4-0 | open | 688 | 160 | 0 | 528 | 1328 | 3292 | Tamas Terlaky | milo | 358152.2621937089* | aggregations variable_bound mixed_binary general_linear |
| milo-v12-6-r1-58-1 | hard | 4440 | 1500 | 0 | 2940 | 9540 | 25068 | Tamas Terlaky | milo | 634081.4112039516 | decomposition aggregations precedence variable_bound mixed_binary general_linear |
| milo-v12-6-r1-75-1 | open | 5698 | 1925 | 0 | 3773 | 12243 | 32174 | Tamas Terlaky | milo | 1153756.39820567* | decomposition aggregations precedence variable_bound mixed_binary general_linear |
Reference
@article{BixbyBoydIndovina1992,
author = {R. E. Bixby and E. A. Boyd and R. R. Indovina},
issue = {2},
journal = {SIAM News},
language = {English},
pages = {16},
title = {{MIPLIB}: {A} Test Set of Mixed Integer Programming Problems},
volume = {25},
year = {1992}
}Last Update 2024 by Julian Manns
generated with R Markdown
© by Zuse Institute Berlin (ZIB)
Imprint