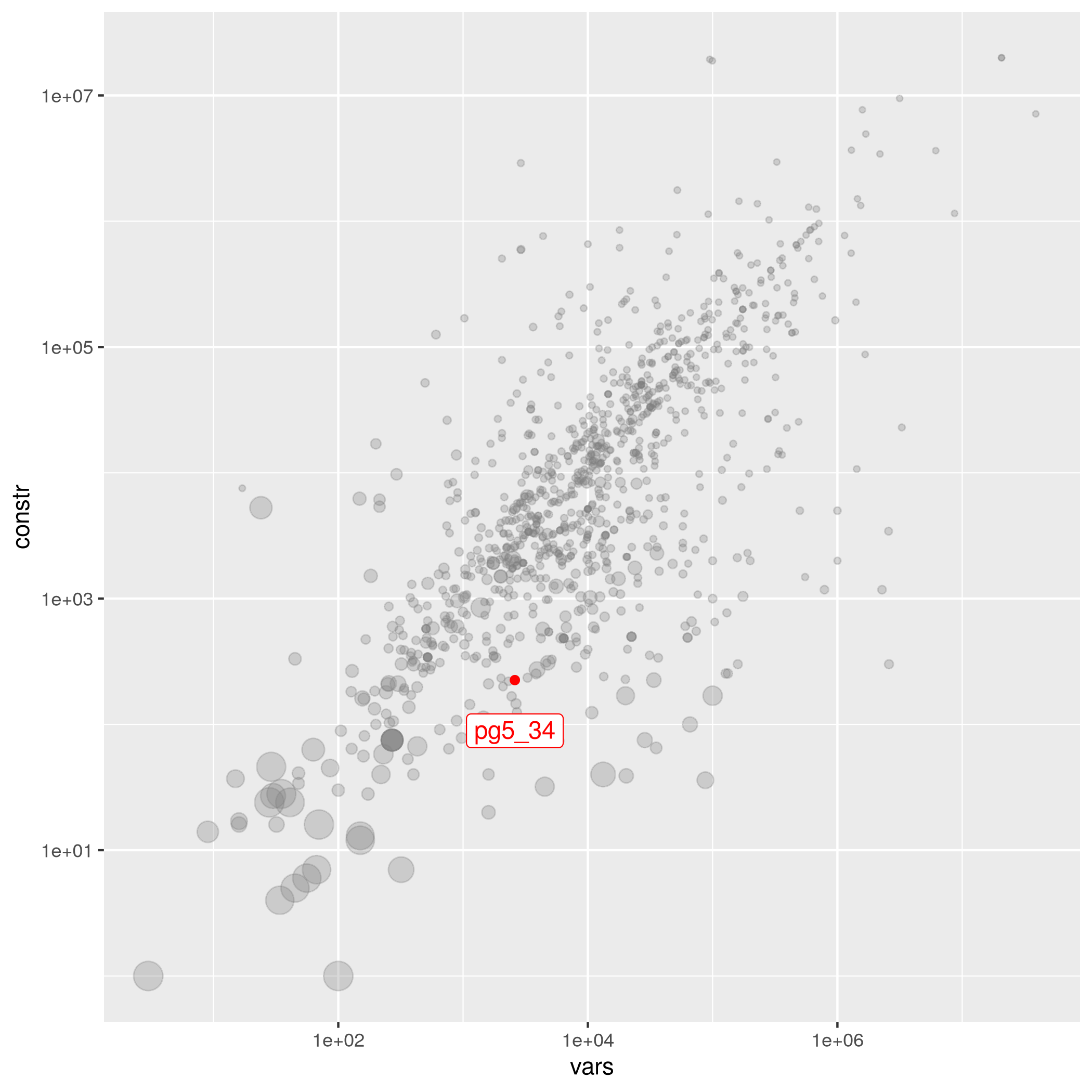
pg5_34

benchmark decomposition benchmark_suitable mixed_binary

Submitter	Variables	Constraints	Density	Status	Group	Objective	MPS File
M. Dawande	2600	225	1.31624e-02	easy	–	-14339.35345	pg5_34.mps.gz

Multiproduct partial shipment model Imported from MIPLIB2010.

Location of instance in collection

Instance Statistics

Detailed explanation of the following tables can be found here.

Size Related Properties
	Original	Presolved
Variables	2600	2600
Constraints	225	225
Binaries	100	100
Integers	0	0
Continuous	2500	2500
Implicit Integers	0	0
Fixed Variables	0	0
Nonzero Density	0.0131624	0.0131624
Nonzeroes	7700	7700

Constraint Classification Properties
	Original	Presolved
Total	225	225
Empty	0	0
Free	0	0
Singleton	0	0
Aggregations	0	0
Precedence	0	0
Variable Bound	0	0
Set Partitioning	0	0
Set Packing	0	0
Set Covering	0	0
Cardinality	0	0
Invariant Knapsack	0	0
Equation Knapsack	0	0
Bin Packing	0	0
Knapsack	0	0
Integer Knapsack	0	0
Mixed Binary	225	225
General Linear	0	0
Indicator	0	0

Structure

Available nonzero structure and decomposition information. Further information can be found here.

Nonzero entries of original problem

Nonzero entries after trivial presolving

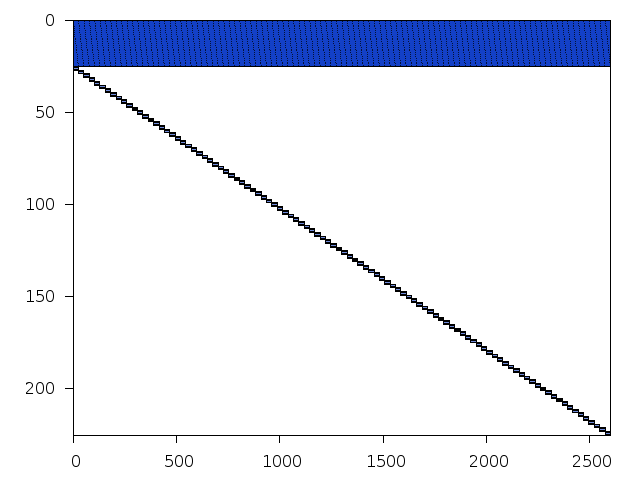
Decomposed structure of original problem (dec-file)

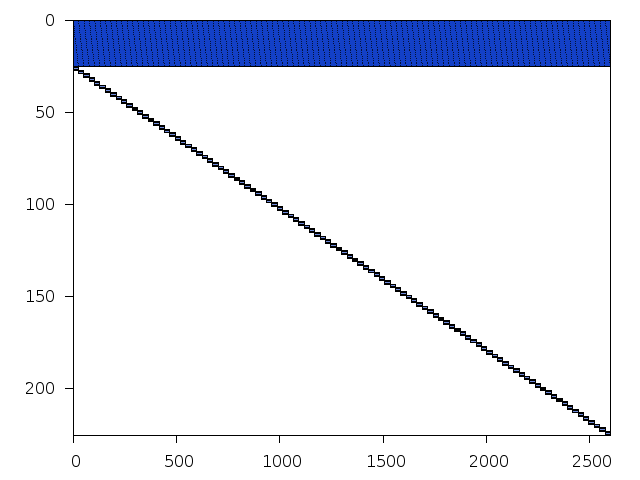
Decomposed structure after trivial presolving (dec-file)

	value	min	median	mean	max
Components	2.004321
Constraint %		0.888889	0.888889	0.888889	0.888889
Variable %		1.000000	1.000000	1.000000	1.000000
Score	0.880000

Best Known Solution(s)

Find solutions below. Download the archive containing all solutions from the Download page.

ID	Objective	Exact	Int. Viol	Cons. Viol	Obj. Viol	Submitter	Date	Description
2	-14339.35	-14339.35	0	0	3.1e-06	-	2018-10-13	Solution found during MIPLIB2017 problem selection.
1	-14339.35	-14339.35	0	0	0.0e+00	-	2018-10-13	Solution imported from MIPLIB2010.

Similar instances in collection

The following instances are most similar to pg5_34 in the collection. This similarity analysis is based on 100 scaled instance features describing properties of the variables, objective function, bounds, constraints, and right hand sides.

Instance	Status	Variables	Binaries	Integers	Continuous	Constraints	Nonz.	Submitter	Group	Objective	Tags
pg	easy	2700	100	0	2600	125	5200	M. Dawande	–	-8674.34260712	benchmark decomposition benchmark_suitable mixed_binary
neos-595904	easy	4508	1148	0	3360	2452	22364	NEOS Server Submission	neos-pseudoapplication-43	64829.59	decomposition benchmark_suitable set_partitioning mixed_binary
nh97_potential	easy	1180	630	328	222	1916	5748	MIPLIB submission pool	–	1418	benchmark_suitable mixed_binary general_linear
pigeon-08	easy	344	272	0	72	601	5176	Sam Allen	pigeon	-7000	benchmark_suitable set_partitioning cardinality invariant_knapsack mixed_binary
pigeon-10	easy	490	400	0	90	931	8150	Sam Allen	pigeon	-9000	benchmark_suitable set_partitioning cardinality invariant_knapsack mixed_binary

Reference

@article{DawandeGavirneniTayur2006,
 author = {M. Dawande and S. Gavirneni and S. Tayur},
 instance = {pg,pg5_34},
 journal = {Operations Research},
 language = {English},
 number = {2},
 pages = {337--352},
 title = {Effective Heuristics for Multiproduct Partial Shipment Models},
 volume = {54},
 year = {2006}
}