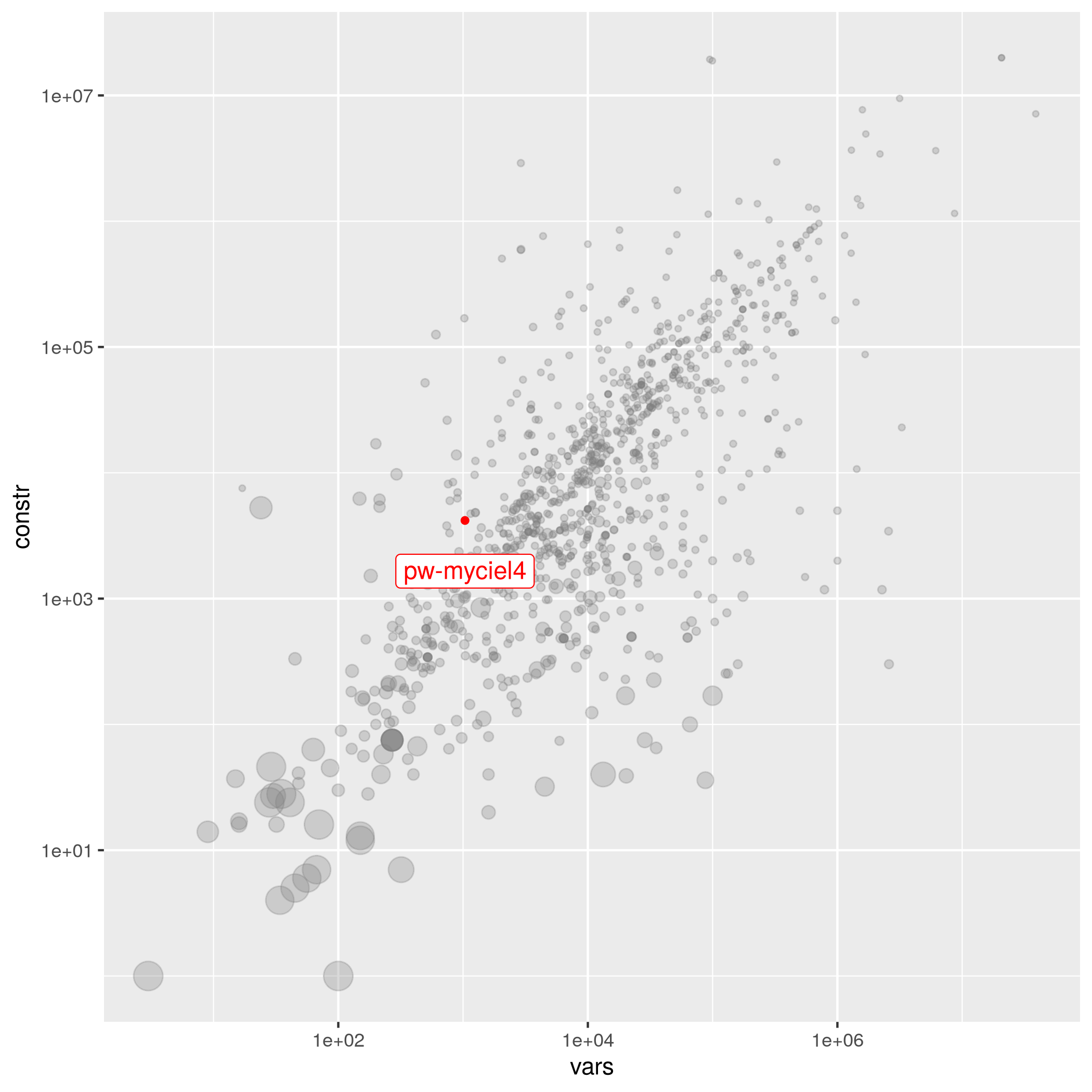
pw-myciel4

benchmark_suitable precedence variable_bound set_partitioning general_linear

Submitter	Variables	Constraints	Density	Status	Group	Objective	MPS File
Arie Koster	1059	8164	2.0564e-03	easy	–	9.999999999999996	pw-myciel4.mps.gz

Model to compute the pathwidth of Mycielski-4 instance from DIMACS graph coloring database Imported from MIPLIB2010.

Location of instance in collection

Instance Statistics

Detailed explanation of the following tables can be found here.

Size Related Properties
	Original	Presolved
Variables	1059	1036
Constraints	8164	4180
Binaries	1058	1035
Integers	1	1
Continuous	0	0
Implicit Integers	0	0
Fixed Variables	0	0
Nonzero Density	0.00205640	0.00226049
Nonzeroes	17779	9789

Constraint Classification Properties
	Original	Presolved
Total	8164	4180
Empty	0	0
Free	0	0
Singleton	0	0
Aggregations	0	0
Precedence	506	483
Variable Bound	7590	3630
Set Partitioning	45	45
Set Packing	0	0
Set Covering	0	0
Cardinality	0	0
Invariant Knapsack	0	0
Equation Knapsack	0	0
Bin Packing	0	0
Knapsack	0	0
Integer Knapsack	0	0
Mixed Binary	0	0
General Linear	23	22
Indicator	0	0

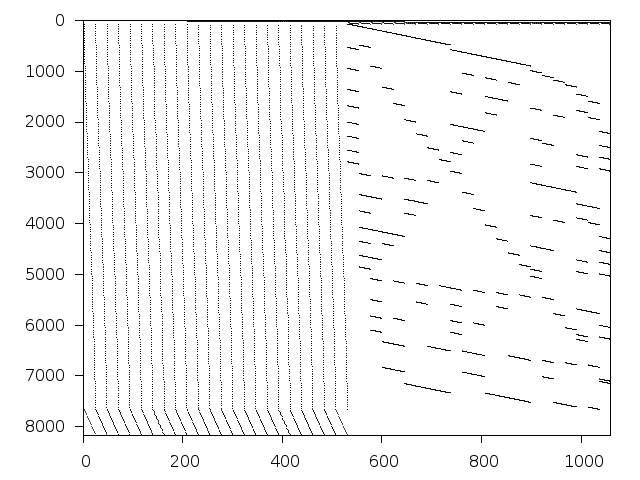
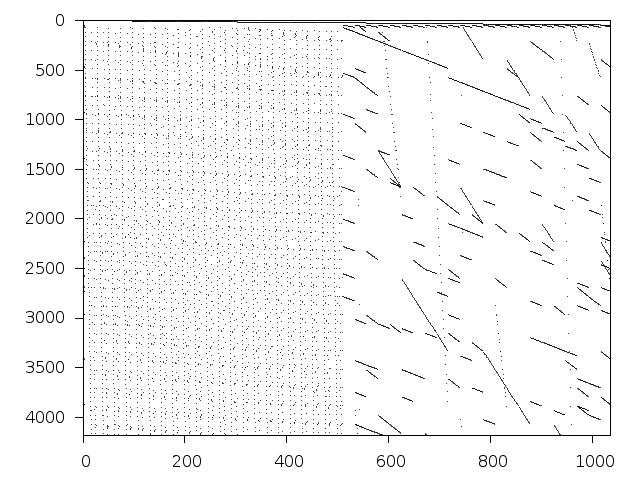
Structure

Available nonzero structure and decomposition information. Further information can be found here.

Nonzero entries of original problem

Nonzero entries after trivial presolving

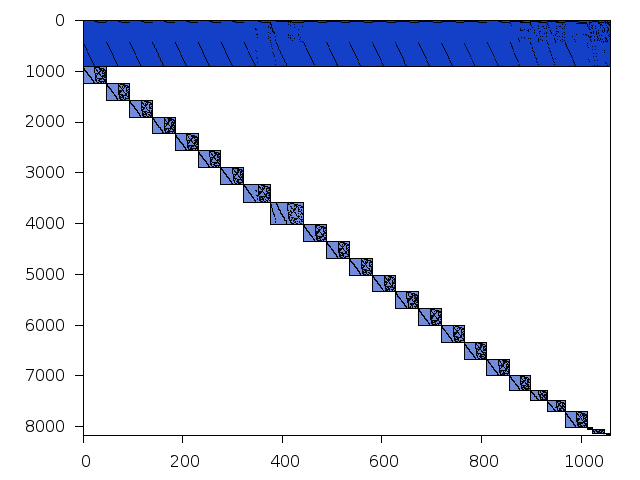
Decomposed structure of original problem (dec-file)

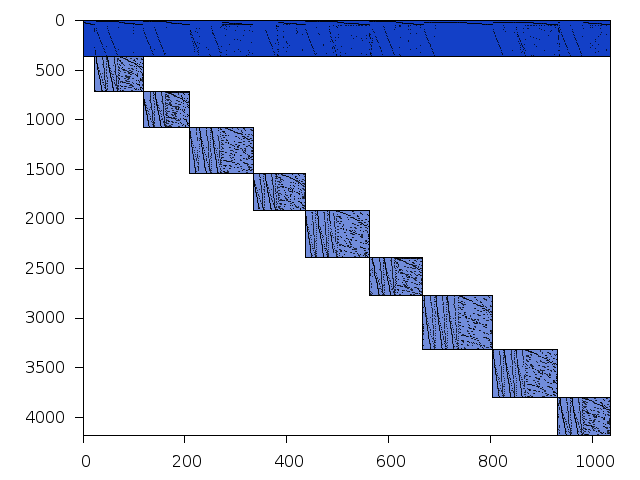
Decomposed structure after trivial presolving (dec-file)

	value	min	median	mean	max
Components	0.301030
Constraint %		98.3971	98.3971	98.3971	98.3971
Variable %		97.6834	97.6834	97.6834	97.6834
Score	0.022795

Best Known Solution(s)

Find solutions below. Download the archive containing all solutions from the Download page.

ID	Objective	Exact	Int. Viol	Cons. Viol	Obj. Viol	Submitter	Date	Description
2	10	10	0	0	0	-	2018-10-13	Solution found during MIPLIB2017 problem selection.
1	10	10	0	0	0	-	2018-10-13	Solution imported from MIPLIB2010.

Similar instances in collection

The following instances are most similar to pw-myciel4 in the collection. This similarity analysis is based on 100 scaled instance features describing properties of the variables, objective function, bounds, constraints, and right hand sides.

Instance	Status	Variables	Binaries	Integers	Continuous	Constraints	Nonz.	Submitter	Group	Objective	Tags
neos-3696678-lyvia	easy	7683	7516	167	0	9004	30452	Jeff Linderoth	neos-pseudoapplication-56	83.74999995899876	decomposition variable_bound set_covering cardinality invariant_knapsack mixed_binary general_linear
tbfp-bigm	hard	2406	2404	0	2	35999	74338	Rob Pratt	–	24.163194443	variable_bound set_partitioning
neos-5041756-cobark	easy	60301	60000	0	301	30900	180900	Jeff Linderoth	neos-pseudoapplication-12	Unbounded	decomposition precedence variable_bound set_packing invariant_knapsack mixed_binary
graphdraw-gemcutter	easy	166	112	16	38	474	1420	Cézar Augusto Nascimento e Silva	graphdraw	7118.5	benchmark_suitable variable_bound set_partitioning invariant_knapsack mixed_binary general_linear
neos-850681	easy	2594	2479	16	99	2067	37113	NEOS Server Submission	neos-pseudoapplication-12	2472	benchmark_suitable aggregations variable_bound set_partitioning set_packing invariant_knapsack general_linear

Reference

No bibliographic information available