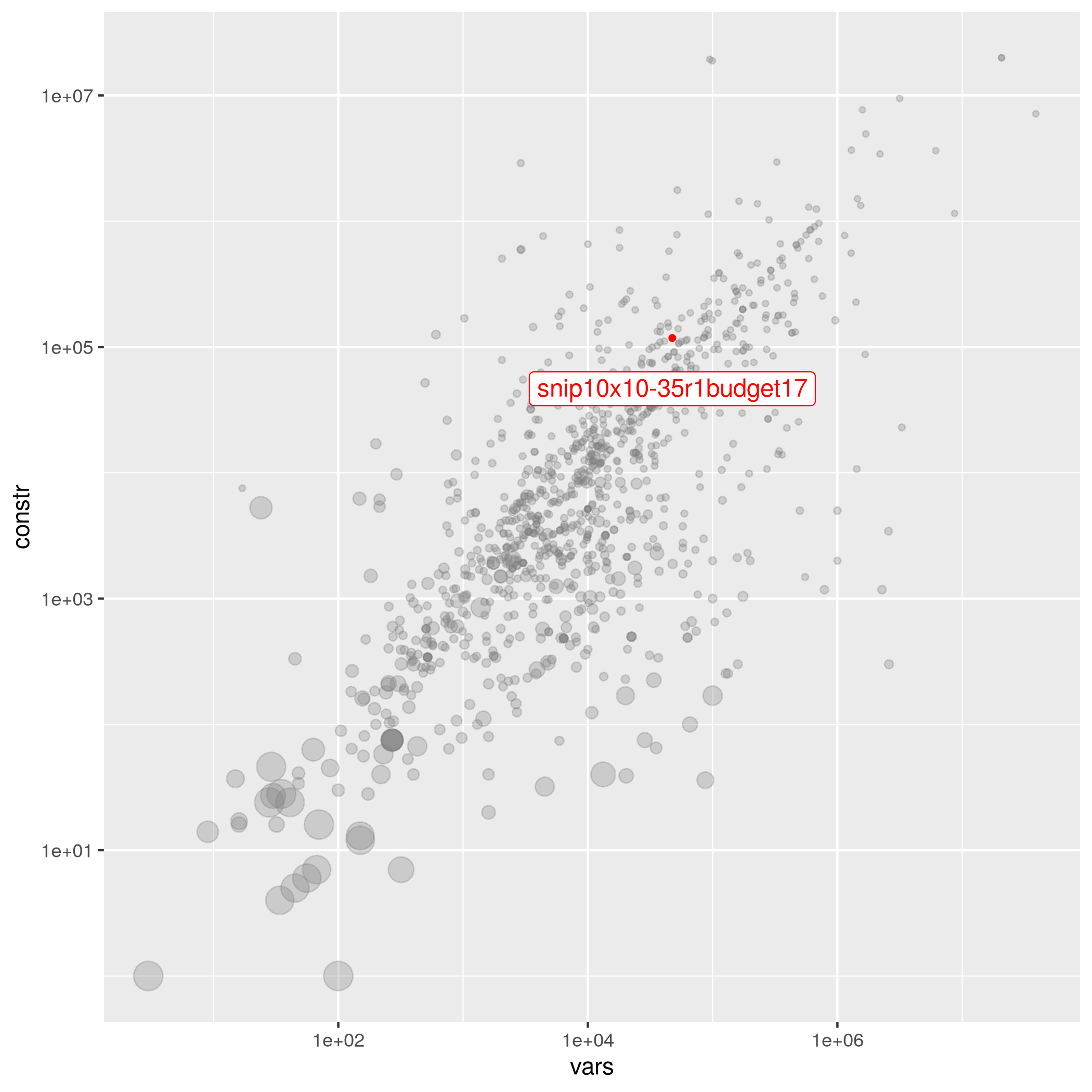
snip10x10-35r1budget17

aggregations variable_bound invariant_knapsack mixed_binary

Submitter	Variables	Constraints	Density	Status	Group	Objective	MPS File
Utz-Uwe Haus	47611	213801	4.66962e-05	hard	–	72.30862035707088	snip10x10-35r1budget17.mps.gz

Exact MILP reformulation using binary decision diagrams to obtain scenario bundles of 2-stage stochastic expected shortest path and expected maximum flow problem with decision dependent scenario probabilities. Notes: * very few binary variables * for each fixing of the binaries a system of equations computing conditioned probabilities remains

Location of instance in collection

Instance Statistics

Detailed explanation of the following tables can be found here.

Size Related Properties
	Original	Presolved
Variables	47611	47542
Constraints	213801	117774
Binaries	63	44
Integers	0	0
Continuous	47548	47498
Implicit Integers	0	0
Fixed Variables	0	0
Nonzero Density	4.66962e-05	6.52454e-05
Nonzeroes	475334	365323

Constraint Classification Properties
	Original	Presolved
Total	213801	117774
Empty	0	0
Free	0	0
Singleton	95069	0
Aggregations	23762	23737
Precedence	0	0
Variable Bound	0	1081
Set Partitioning	0	0
Set Packing	0	0
Set Covering	0	0
Cardinality	0	0
Invariant Knapsack	1	1
Equation Knapsack	0	0
Bin Packing	0	0
Knapsack	0	0
Integer Knapsack	0	0
Mixed Binary	94969	92955
General Linear	0	0
Indicator	0	0

Structure

Available nonzero structure and decomposition information. Further information can be found here.

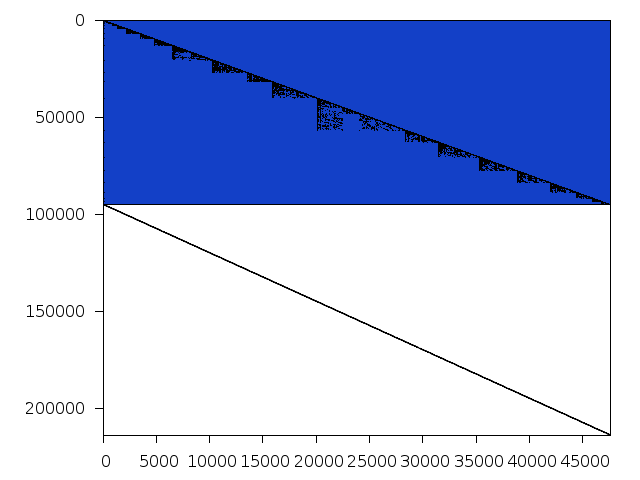
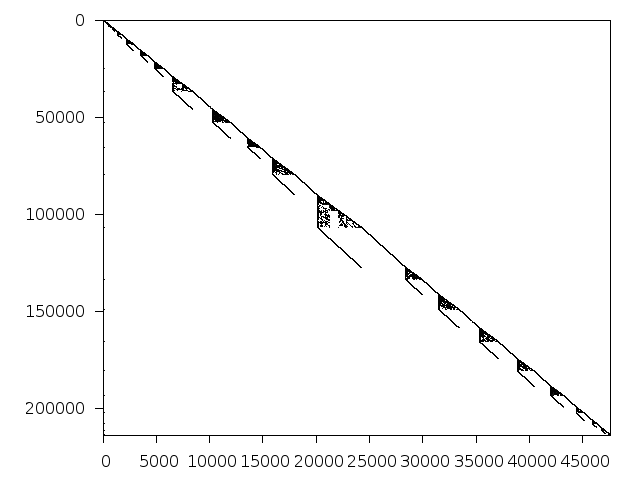
Nonzero entries of original problem

Nonzero entries after trivial presolving

Decomposed structure of original problem (dec-file)

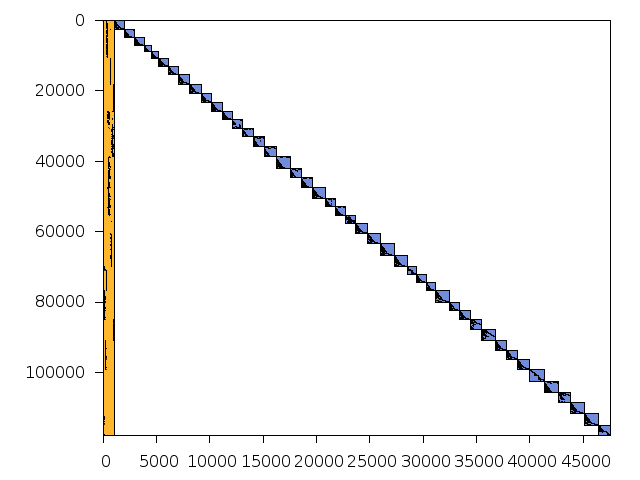
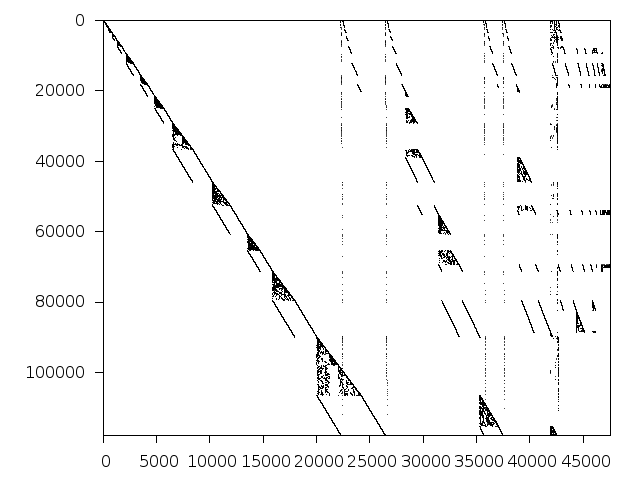
Decomposed structure after trivial presolving (dec-file)

	value	min	median	mean	max
Components	0.301030
Constraint %		79.8451	79.8451	79.8451	79.8451
Variable %		50.0463	50.0463	50.0463	50.0463
Score	0.398856

Best Known Solution(s)

Find solutions below. Download the archive containing all solutions from the Download page.

## Warning in lapply(df["exactobjval"], as.numeric): NAs introduced by coercion

ID	Objective	Exact	Cons. Viol	Submitter	Date	Description
4	72.30862		3e-07	Hans Mittelmann	2020-01-09	Solved with Gurobi 9.0 using 80 Threads within 21 hours
3	72.30849		8e-07	Edward Rothberg	2019-12-13	Obtained with Gurobi 9.0
2	72.30869		1e-06	Robert Ashford and Alkis Vazacopoulus	2019-12-18	Found using ODH\|CPlex
1	73.82347	73.82348	1e-06	-	2018-10-13	Solution found during MIPLIB2017 problem selection.

Similar instances in collection

The following instances are most similar to snip10x10-35r1budget17 in the collection. This similarity analysis is based on 100 scaled instance features describing properties of the variables, objective function, bounds, constraints, and right hand sides.

Instance	Status	Variables	Binaries	Continuous	Constraints	Nonz.	Submitter	Group	Objective	Tags
istanbul-no-cutoff	easy	5282	30	5252	20346	71477	Utz-Uwe Haus	–	204.08170701	benchmark benchmark_suitable aggregations variable_bound knapsack mixed_binary
net12	easy	14115	1603	12512	14021	80384	P. Belotti	–	214	benchmark decomposition benchmark_suitable precedence set_packing cardinality invariant_knapsack mixed_binary
neos-5188808-nattai	easy	14544	288	14256	29452	133686	Jeff Linderoth	neos-pseudoapplication-98	0.110283622999984	benchmark decomposition benchmark_suitable aggregations precedence variable_bound set_partitioning cardinality knapsack mixed_binary
neos-691058	easy	3006	1755	1251	2667	30837	NEOS Server Submission	neos-pseudoapplication-110	296.999999999986	benchmark_suitable set_partitioning cardinality mixed_binary
nsa	easy	388	36	352	1297	4204	MIPLIB submission pool	–	120	decomposition benchmark_suitable aggregations mixed_binary

Reference

@TechReport{haus-michini-laumanns:17-arxiv,
  author =   {Utz-Uwe Haus and Carla Michini and Marco Laumanns},
  title =    {Scenario Aggregation using Binary Decision Diagrams
                  for Stochastic Programs with Endogenous Uncertainty},
  institution =  {arxiv.org},
  year =     2017,
  type =     {arxiv eprint},
  number =   {arXiv:1701.04055}
}