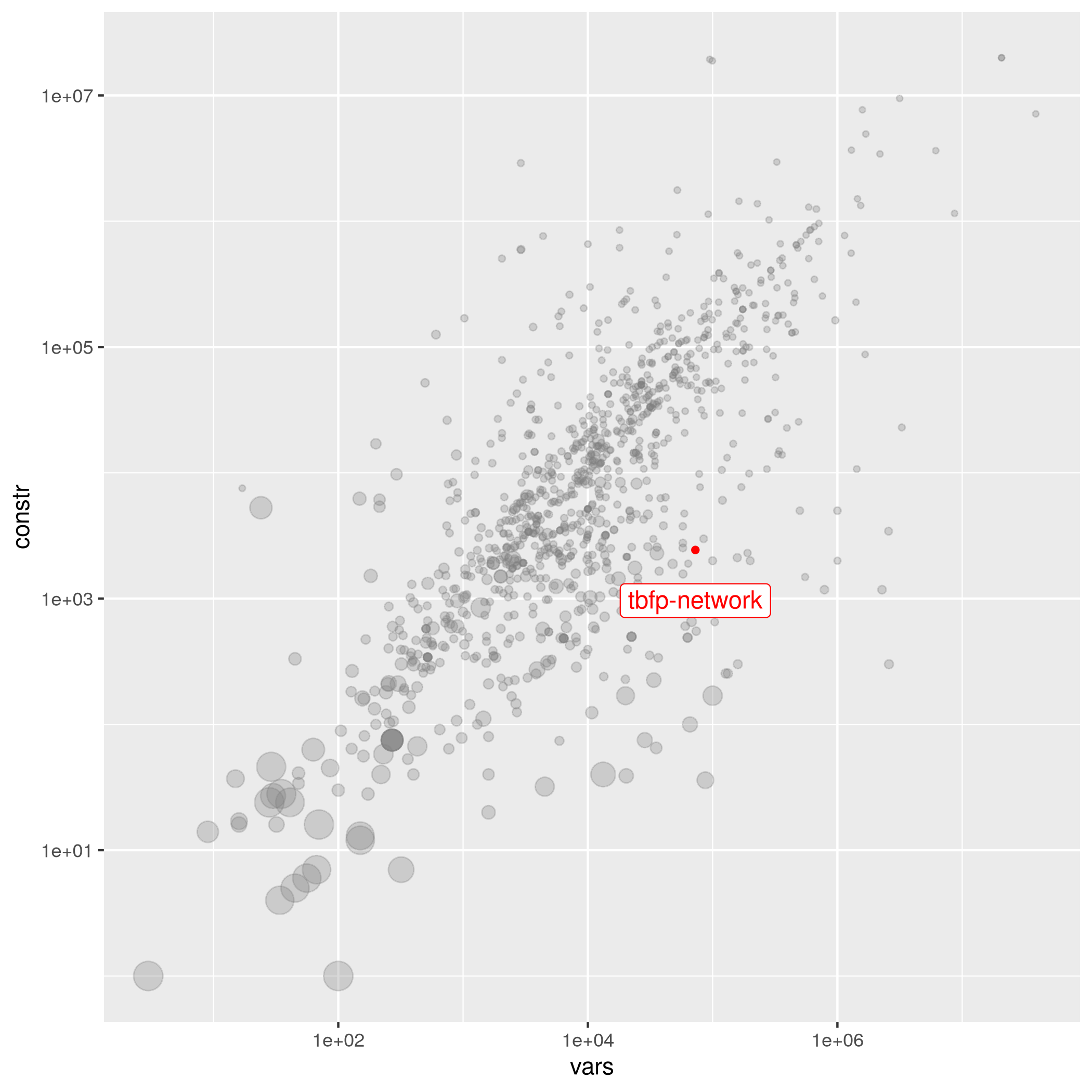
tbfp-network

benchmark binary benchmark_suitable set_partitioning cardinality

Submitter	Variables	Constraints	Density	Status	Group	Objective	MPS File
Rob Pratt	72747	2436	1.21796e-03	easy	–	24.16319444	tbfp-network.mps.gz

Two formulations (big-M and network-based) for traveling baseball fan problem. Uses data from 2014 Major League Baseball regular season. Paper uses 2014 data: https://support.sas.com/resources/papers/proceedings14/SAS101-2014.pdf Blog post uses 2015 data: https://blogs.sas.com/content/operations/2015/04/03/the-traveling-baseball-fan-problem/

Location of instance in collection

Instance Statistics

Detailed explanation of the following tables can be found here.

Size Related Properties
	Original	Presolved
Variables	72747	72747
Constraints	2436	2436
Binaries	72747	72747
Integers	0	0
Continuous	0	0
Implicit Integers	0	0
Fixed Variables	0	0
Nonzero Density	0.00121796	0.00121796
Nonzeroes	215837	215837

Constraint Classification Properties
	Original	Presolved
Total	2436	2436
Empty	0	0
Free	0	0
Singleton	0	0
Aggregations	0	0
Precedence	0	0
Variable Bound	0	0
Set Partitioning	42	58
Set Packing	0	0
Set Covering	0	0
Cardinality	2394	2378
Invariant Knapsack	0	0
Equation Knapsack	0	0
Bin Packing	0	0
Knapsack	0	0
Integer Knapsack	0	0
Mixed Binary	0	0
General Linear	0	0
Indicator	0	0

Structure

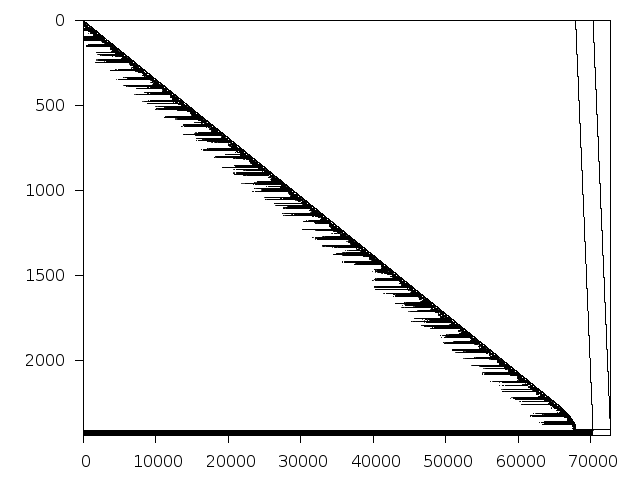
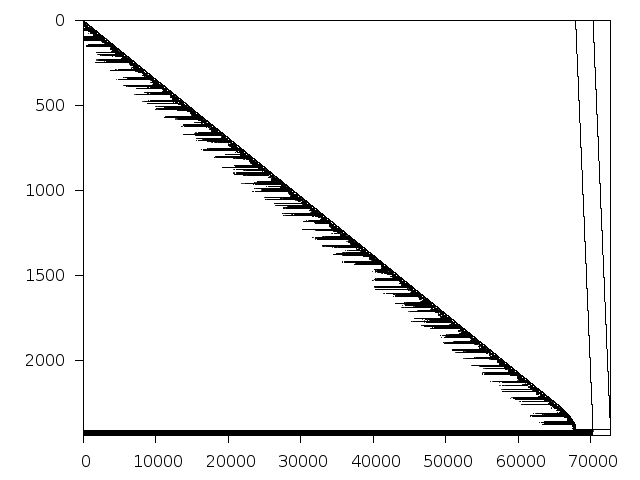
Available nonzero structure and decomposition information. Further information can be found here.

Nonzero entries of original problem

Nonzero entries after trivial presolving

Decomposed structure of original problem (dec-file)

Decomposed structure after trivial presolving (dec-file)

	value	min	median	mean	max
Components	0.301030
Constraint %		97.6190	97.6190	97.6190	97.6190
Variable %		99.9285	99.9285	99.9285	99.9285
Score	0.000698

Best Known Solution(s)

Find solutions below. Download the archive containing all solutions from the Download page.

ID	Objective	Exact	Int. Viol	Cons. Viol	Obj. Viol	Submitter	Date	Description
1	24.16319	24.16319	0	0	0	-	2018-10-11	Solution found during MIPLIB2017 problem selection.

Similar instances in collection

The following instances are most similar to tbfp-network in the collection. This similarity analysis is based on 100 scaled instance features describing properties of the variables, objective function, bounds, constraints, and right hand sides.

Instance	Status	Variables	Binaries	Integers	Constraints	Nonz.	Submitter	Group	Objective	Tags
neos-4531126-vouga	open	169996	169996	0	7694	967980	Jeff Linderoth	neos-pseudoapplication-87	525030.8846192999*	binary decomposition numerics set_partitioning cardinality invariant_knapsack binpacking mixed_binary
datt256	open	262144	262144	0	11077	1503732	Jon Dattorro	–		no_solution binary set_partitioning cardinality
s100	hard	364417	364417	0	14733	1777917	Daniel Espinoza	Spinoza	-0.1697235270583	benchmark binary benchmark_suitable aggregations set_partitioning set_packing cardinality invariant_knapsack knapsack
supportcase6	easy	130052	130051	1	771	584976	Michael Winkler	–	51906.47737	benchmark benchmark_suitable set_partitioning cardinality general_linear
nu120-pr9	easy	7350	7308	42	2220	22176	MIPLIB submission pool	nus-prxy	24945	decomposition numerics aggregations variable_bound cardinality general_linear

Reference

@INPROCEEDINGS{ChapmanGalatiPratt2014,
  author = {Tonya Chapman and Matt Galati and Rob Pratt},
  title = {The Traveling Baseball Fan Problem and the OPTMODEL Procedure},
  booktitle = {Proceedings of the SAS Global Forum 2014 Conference},
  year = {2014},
  address = {Cary, NC},
  publisher = {SAS Institute Inc.},
  note = {\url{http://support.sas.com/resources/papers/proceedings14/SAS101-2014.pdf}}
}