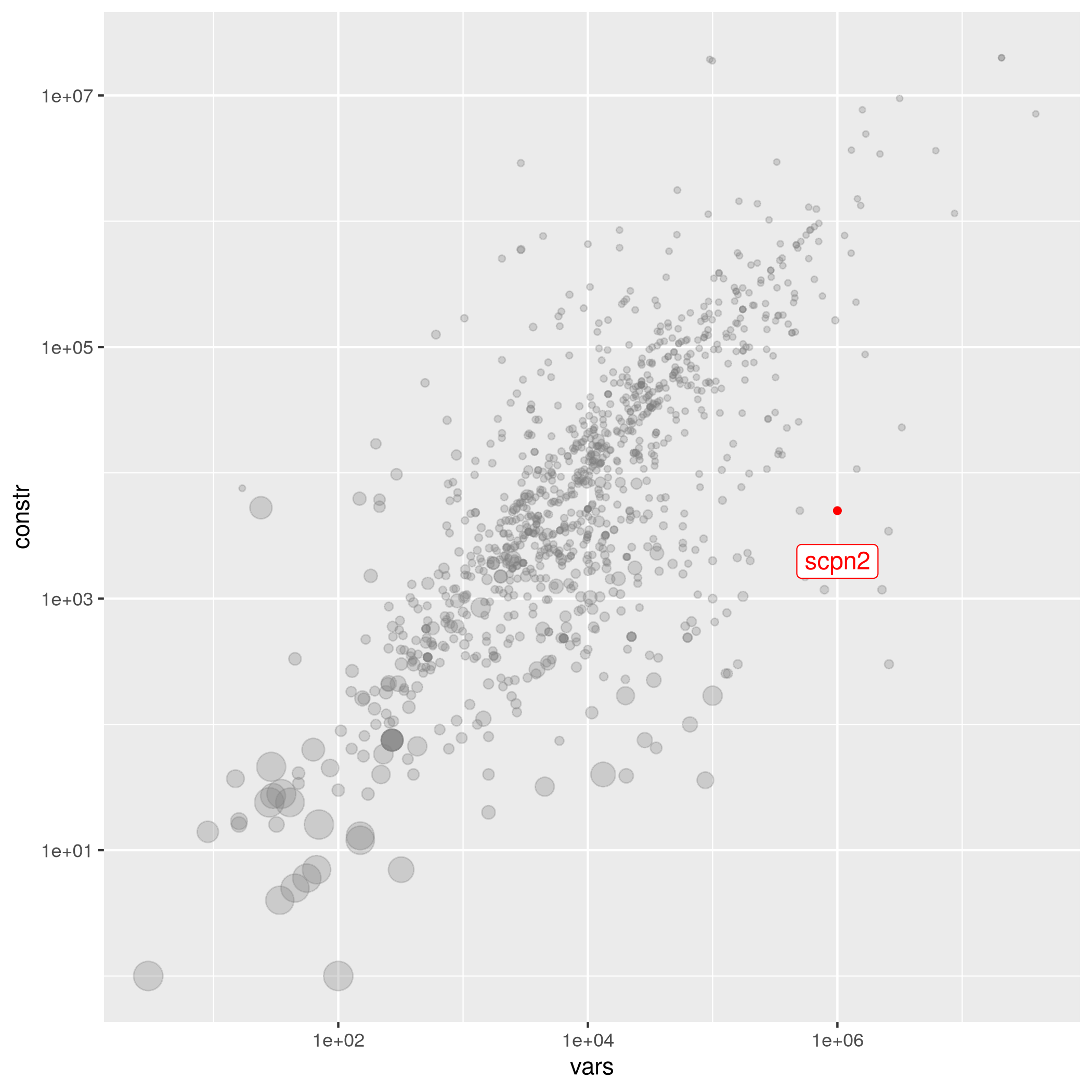
scpn2

binary set_covering

Submitter Variables Constraints Density Status Group Objective MPS File
Shunji Umetani 1000000 5000 2.5e-03 open scp 489.0* scpn2.mps.gz

This is a random test instance generator for SCP using the scheme of the following paper, namely the column cost c[j] are integer randomly generated from [1,100]; every column covers at least one row; and every row is covered by at least two columns. see reference: E. Balas and A. Ho, Set covering algorithms using cutting planes, heuristics, and subgradient optimization: A computational study, Mathematical Programming, 12 (1980), 37-60. We have newly generated Classes I-N with the following parameter values, where each class has five instances. We have also generated reduced instances by a standard pricing method in the following paper: S. Umetani and M. Yagiura, Relaxation heuristics for the set covering problem, Journal of the Operations Research Society of Japan, 50 (2007), 350-375. You can obtain the instance generator program from the following web site. https://sites.google.com/site/shunjiumetani/benchmark

Location of instance in collection

Location of instance in collection

Instance Statistics

Detailed explanation of the following tables can be found here.

Size Related Properties
Original Presolved
Variables 1e+06 1e+06
Constraints 5000 5000
Binaries 1e+06 1e+06
Integers 0 0
Continuous 0 0
Implicit Integers 0 0
Fixed Variables 0 0
Nonzero Density 0.0025 0.0025
Nonzeroes 12500000 12500000
Constraint Classification Properties
Original Presolved
Total 5000 5000
Empty 0 0
Free 0 0
Singleton 0 0
Aggregations 0 0
Precedence 0 0
Variable Bound 0 0
Set Partitioning 0 0
Set Packing 0 0
Set Covering 5000 5000
Cardinality 0 0
Invariant Knapsack 0 0
Equation Knapsack 0 0
Bin Packing 0 0
Knapsack 0 0
Integer Knapsack 0 0
Mixed Binary 0 0
General Linear 0 0
Indicator 0 0

Structure

Available nonzero structure and decomposition information. Further information can be found here.

Nonzero entries of original problem

Nonzero entries of original problem

Matrix after trivial presolving

Nonzero entries after trivial presolving

Decomposed structure of original problem

Decomposed structure of original problem (dec-file)

Decomposed structure after trivial presolving

Decomposed structure after trivial presolving (dec-file)

value min median mean max
Components 0.30103
Constraint % 100 100 100 100
Variable % 100 100 100 100
Score 0.00000

Best Known Solution(s)

Find solutions below. Download the archive containing all solutions from the Download page.

## Warning in lapply(df["exactobjval"], as.numeric): NAs introduced by coercion
ID Objective Exact Int. Viol Cons. Viol Obj. Viol Submitter Date Description
9 490 490 0 0 0 Peng Lin, Shaowei Cai, Mengchuan Zou, Jinkun Lin 2023-05-03 Computed by local search based on the paper Peng Lin, Shaowei Cai, Mengchuan Zou, and Jinkun Lin. “New Characterizations and Efficient Local Search for General Integer Linear Programming”, arXiv preprint arXiv:2305.00188 (2023).
8 499 499 0 0 0 Ed Rothberg 2023-03-20 Found with the Gurobi 10.0 NoRel heuristic, starting from the previous solution at 501.
7 500 500 0 0 0 Ed Rothberg 2023-01-06 Found using Gurobi 10.0 NoRel heuristic, starting from the solution at 501.
6 501 501 0 0 0 Yuya Hattori 2022-11-16 Computed by local search based on the paper M. Yagiura, M. Kishida and T. Ibaraki, “A 3-Flip Neighborhood Local Search for the Set Covering Problem”, European Journal of Operational Research, 172 (2006) 472-499.
5 515 515 0 0 0 Yuji Koguma 2022-09-13 Computed with weighting tabu search.
4 516 516 0 0 0 Yuji Koguma 2020-09-30 Obtained with a Tabu Search algorithm based on the paper, Koji Nonobe, Toshihide Ibaraki: “An Improved Tabu Search Method For The Weighted Constraint Satisfaction Problem,” INFOR, Vol.39, No.2, pp.131-151, 2001.
3 528 528 0 0 0 Shunsuke Kamiya 2020-05-17 Computed with weighting local search with exploiting variable associations (WLS) Umetani, Shunji. “Exploiting variable associations to configure efficient local search algorithms in large-scale binary integer programs.” European Journal of Operational Research 263.1 (2017): 72-81.
2 534 0 0 0 Robert Ashford and Alkis Vazacopoulus 2019-12-18 Found using ODH|CPlex
10 489 489 0 0 0 Mars Davletshin 2023-12-09 It was obtained with Huawei OptVerse solver (version 0.6.0) using neural primal heuristic and large neighborhood search.
1 540 540 0 0 0 - 2018-10-12 Solution found during MIPLIB2017 problem selection.

Similar instances in collection

The following instances are most similar to scpn2 in the collection. This similarity analysis is based on 100 scaled instance features describing properties of the variables, objective function, bounds, constraints, and right hand sides.

Instance Status Variables Binaries Integers Continuous Constraints Nonz. Submitter Group Objective Tags
scpm1 open 500000 500000 0 0 5000 6250000 Shunji Umetani scp 540.0* binary set_covering
scpl4 open 200000 200000 0 0 2000 2000000 Shunji Umetani scp 259.0* binary set_covering
scpj4scip open 99947 99947 0 0 1000 999893 Shunji Umetani scp 128* binary set_covering
scpk4 open 100000 100000 0 0 2000 1000000 Shunji Umetani scp 318.0* binary set_covering
neos-5052403-cygnet easy 32868 32868 0 0 38268 4898304 Jeff Linderoth neos-pseudoapplication-100 182 benchmark binary benchmark_suitable set_covering invariant_knapsack

Reference

No bibliographic information available
Last Update 2024 by Julian Manns
generated with R Markdown
© by Zuse Institute Berlin (ZIB)
Imprint