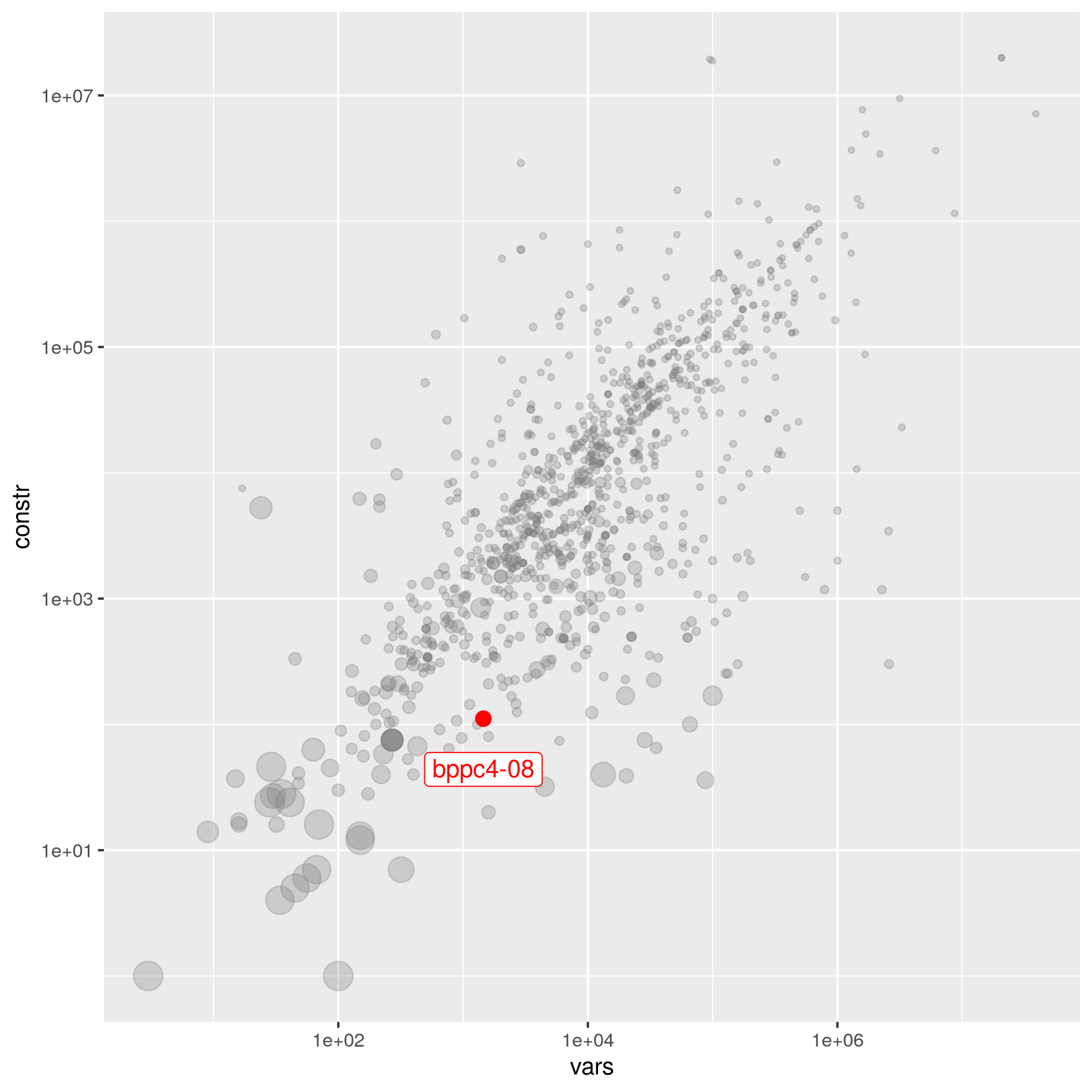
bppc4-08
benchmark benchmark_suitable set_partitioning mixed_binary
| Submitter | Variables | Constraints | Density | Status | Group | Objective | MPS File |
|---|---|---|---|---|---|---|---|
| Manuel Iori | 1456 | 111 | 1.48277e-01 | easy | bppc | 53 | bppc4-08.mps.gz |
The models that we attach solve the “bar-relaxation”, also known as the “Bin Packing Problem with Contiguity” or the “P||Cmax with contiguity”. This is one of the most interesting relaxations for two dimensional cutting and packing problems. Its solution by means of an ILP software is the bottleneck of the primal decomposition methods that we attempted in the paper cited below. In detail, the files correspond to model (12)-(15) in the paper, applied to the instances of the Classes 4, 6 and 8 by Martello and Vigo (Management Science, 1998).
Instance Statistics
Detailed explanation of the following tables can be found here.
| Original | Presolved | |
|---|---|---|
| Variables | 1456 | 1455 |
| Constraints | 111 | 111 |
| Binaries | 1454 | 1454 |
| Integers | 0 | 0 |
| Continuous | 2 | 1 |
| Implicit Integers | 0 | 0 |
| Fixed Variables | 1 | 0 |
| Nonzero Density | 0.148277 | 0.148379 |
| Nonzeroes | 23964 | 23964 |
| Original | Presolved | |
|---|---|---|
| Total | 111 | 111 |
| Empty | 0 | 0 |
| Free | 0 | 0 |
| Singleton | 0 | 0 |
| Aggregations | 0 | 0 |
| Precedence | 0 | 0 |
| Variable Bound | 0 | 0 |
| Set Partitioning | 20 | 20 |
| Set Packing | 0 | 0 |
| Set Covering | 0 | 0 |
| Cardinality | 0 | 0 |
| Invariant Knapsack | 0 | 0 |
| Equation Knapsack | 0 | 0 |
| Bin Packing | 0 | 0 |
| Knapsack | 0 | 0 |
| Integer Knapsack | 0 | 0 |
| Mixed Binary | 91 | 91 |
| General Linear | 0 | 0 |
| Indicator | 0 | 0 |
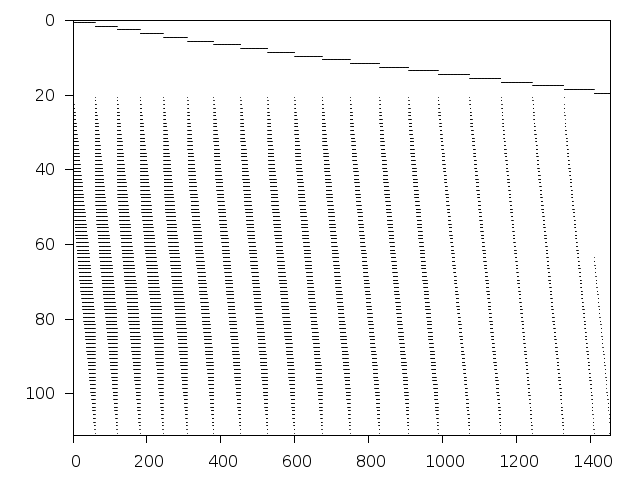
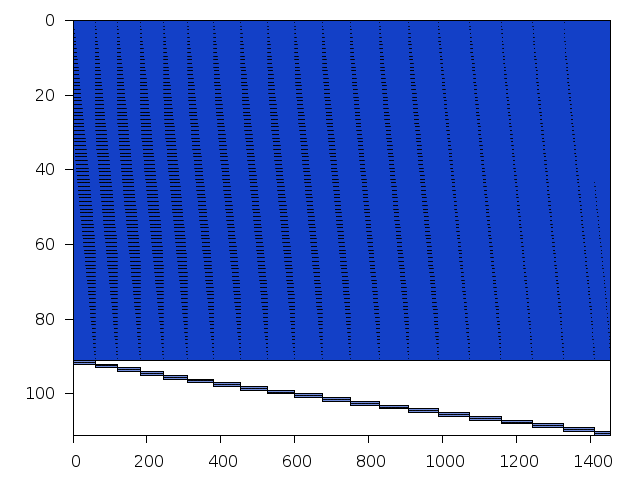
Structure
Available nonzero structure and decomposition information. Further information can be found here.
Decomposed structure of original problem (dec-file)
Decomposed structure after trivial presolving (dec-file)
| value | min | median | mean | max | |
|---|---|---|---|---|---|
| Components | 1.322219 | ||||
| Constraint % | 0.900901 | 0.900901 | 0.900901 | 0.900901 | |
| Variable % | 3.024050 | 4.996560 | 5.085910 | 5.841920 | |
| Score | 0.171177 |
Best Known Solution(s)
Find solutions below. Download the archive containing all solutions from the Download page.
| ID | Objective | Exact | Int. Viol | Cons. Viol | Obj. Viol | Submitter | Date | Description |
|---|---|---|---|---|---|---|---|---|
| 1 | 53 | 53 | 0 | 0 | 0 | - | 2018-10-12 | Solution found during MIPLIB2017 problem selection. |
Similar instances in collection
The following instances are most similar to bppc4-08 in the collection. This similarity analysis is based on 100 scaled instance features describing properties of the variables, objective function, bounds, constraints, and right hand sides.
| Instance | Status | Variables | Binaries | Integers | Continuous | Constraints | Nonz. | Submitter | Group | Objective | Tags |
|---|---|---|---|---|---|---|---|---|---|---|---|
| bppc6-02 | hard | 4784 | 4782 | 0 | 2 | 309 | 188143 | Manuel Iori | bppc | 116 | set_partitioning mixed_binary |
| bppc8-09 | easy | 431 | 423 | 6 | 2 | 67 | 9051 | Manuel Iori | bppc | 471.9999999999998 | benchmark_suitable set_partitioning mixed_binary |
| bppc6-06 | open | 3922 | 3920 | 0 | 2 | 273 | 181510 | Manuel Iori | bppc | 208* | set_partitioning mixed_binary |
| assign1-10-4 | open | 572 | 520 | 0 | 52 | 582 | 28280 | Robert Fourer | assign1 | 422* | set_partitioning cardinality mixed_binary |
| assign1-5-8 | easy | 156 | 130 | 0 | 26 | 161 | 3720 | Robert Fourer | assign1 | 211.999999999998 | benchmark benchmark_suitable set_partitioning cardinality mixed_binary |
Reference
@ARTICLE{CDI14,
AUTHOR = "C{\^o}t{\'e}, J.-F. and Dell'Amico, M. and Iori, M.",
TITLE = "Combinatorial {B}enders' Cuts for the Strip Packing Problem",
JOURNAL = "Operations Research",
YEAR = 2014,
VOLUME = 62,
NUMBER = 3,
PAGES = "643--661"
}Last Update 2024 by Julian Manns
generated with R Markdown
© by Zuse Institute Berlin (ZIB)
Imprint