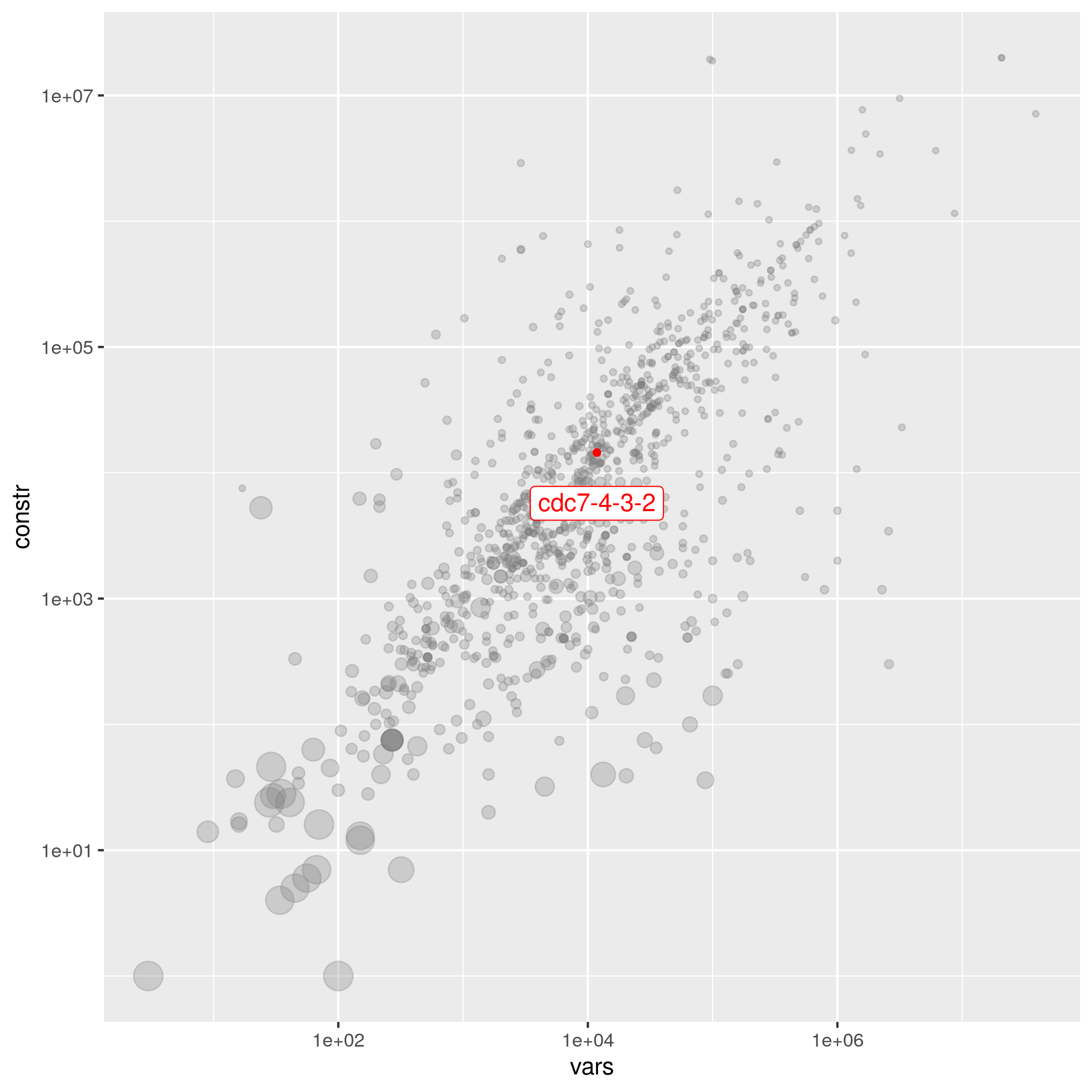
cdc7-4-3-2

binary set_packing

Submitter	Variables	Constraints	Density	Status	Group	Objective	MPS File
Sascha Kurz	11811	14478	1.51955e-03	open	–	-296.0*	cdc7-4-3-2.mps.gz

Codes for Networkcoding A constant dimension code with parameters n, k, d and q is a collection of k-dimensional subspaces of the n-dimensional vector space \(GF(q)^n\) over a finite field with q elements, called codewords, such that the dimension of the intersection of each pair of different k-dimensional subspaces is at most \(k-d/2\). Let \(A_q(n,d;k)\) denote the maximum number of codewords. For instance cdc6-4-3-2 \(A_2(6,4;3)=77\) is known , while \(333 \le A_2(7,4;3) \le 381\) for instance cdc7-4-3-2 are the tightest known bounds, see e.g. . A code of size 381 would correspond to a putative binary q-analog of the Fano plane (finite projective plane of order 2 with 7 points and lines). More bounds are available at http://subspacecodes.uni-bayreuth.de.

Location of instance in collection

Instance Statistics

Detailed explanation of the following tables can be found here.

Size Related Properties
	Original	Presolved
Variables	11811	11811
Constraints	14478	14478
Binaries	11811	11811
Integers	0	0
Continuous	0	0
Implicit Integers	0	0
Fixed Variables	0	0
Nonzero Density	0.00151955	0.00151955
Nonzeroes	259842	259842

Constraint Classification Properties
	Original	Presolved
Total	14478	14478
Empty	0	0
Free	0	0
Singleton	0	0
Aggregations	0	0
Precedence	0	0
Variable Bound	0	0
Set Partitioning	0	0
Set Packing	14478	14478
Set Covering	0	0
Cardinality	0	0
Invariant Knapsack	0	0
Equation Knapsack	0	0
Bin Packing	0	0
Knapsack	0	0
Integer Knapsack	0	0
Mixed Binary	0	0
General Linear	0	0
Indicator	0	0

Structure

Available nonzero structure and decomposition information. Further information can be found here.

Nonzero entries of original problem

Nonzero entries after trivial presolving

Decomposed structure of original problem (dec-file)

Decomposed structure after trivial presolving (dec-file)

	value	min	median	mean	max
Components	0.30103
Constraint %		100	100	100	100
Variable %		100	100	100	100
Score	0.00000

Best Known Solution(s)

Find solutions below. Download the archive containing all solutions from the Download page.

## Warning in lapply(df["exactobjval"], as.numeric): NAs introduced by coercion

ID	Objective	Exact	Submitter	Date	Description
9	-296	-296	Taishi Maeda and Ryuhei Miyashiro	2023-02-06	Obtained with Fixstars Amplify Annealing Engine, a GPU-based QUBO solver.
8	-294	-294	Peng Lin, Shaowei Cai, Mengchuan Zou, Jinkun Lin	2023-05-03	Computed by local search based on the paper Peng Lin, Shaowei Cai, Mengchuan Zou, and Jinkun Lin. “New Characterizations and Efficient Local Search for General Integer Linear Programming”, arXiv preprint arXiv:2305.00188 (2023).
7	-289	-289	Yuji Koguma	2020-06-24	Obtained with a Tabu Search algorithm based on the paper, Koji Nonobe, Toshihide Ibaraki: "An Improved Tabu Search Method For The Weighted Constraint Satisfaction Problem," INFOR, Vol.39, No.2, pp.131-151, 2001
6	-288	-288	Shunsuke Kamiya	2020-05-17	Computed with weighting local search with exploiting variable associations (WLS) ([1]) [1] Umetani, Shunji. “Exploiting variable associations to configure efficient local search algorithms in large-scale binary integer programs.” European Journal of Operational Research 263.1 (2017): 72-81.
5	-285	-285	Edward Rothberg	2020-04-22	Obtained with Gurobi 9.0 using the solution improvement heuristic
4	-282	-282	Frederic Didier	2020-01-22	Obtained with Google OR-tools using 8 Threads through generating subproblems by fixing part of the current solution and trying to solve them with a sub CP-SAT solver
3	-279		Edward Rothberg	2019-12-13	Obtained with Gurobi 9.0
2	-275		Robert Ashford and Alkis Vazacopoulus	2019-12-18	Found using ODH\|CPlex
1	-260	-260	-	2018-10-13	Solution found during MIPLIB2017 problem selection.

Similar instances in collection

The following instances are most similar to cdc7-4-3-2 in the collection. This similarity analysis is based on 100 scaled instance features describing properties of the variables, objective function, bounds, constraints, and right hand sides.

Instance	Status	Variables	Binaries	Constraints	Nonz.	Submitter	Group	Objective	Tags
cod105	easy	1024	1024	1024	57344	MIPLIB submission pool	–	-12	benchmark binary benchmark_suitable set_packing
a2864-99blp	open	200787	200787	22117	20078717	Daniel Heinlein	selofsubspaces	-257*	binary set_packing invariant_knapsack
sorrell8	easy	2046	2046	18944	37888	Toni Sorrell	independentset	-350	binary decomposition variable_bound
sorrell7	open	2048	2048	78848	157696	Toni Sorrell	independentset	-198.0*	binary variable_bound
z26	open	17937	17937	850513	1715613	Daniel Bienstock	–	-1195.0*	binary variable_bound set_packing

Reference

@article{honold2015optimal,
  title={Optimal binary subspace codes of length 6, constant dimension 3 and minimum subspace distance 4},
  author={Honold, Thomas and Kiermaier, Michael and Kurz, Sascha},
  journal={Contemporary Mathematics},
  volume={632},
  pages={157--172},
  year={2015},
}

@incollection{kohnert2008construction,
  title={Construction of large constant dimension codes with a prescribed minimum distance},
  author={Kohnert, Axel and Kurz, Sascha},
  booktitle={Mathematical Methods in Computer Science},
  volume={5393},
  pages={31--42},
  year={2008},
  publisher={Springer}
}