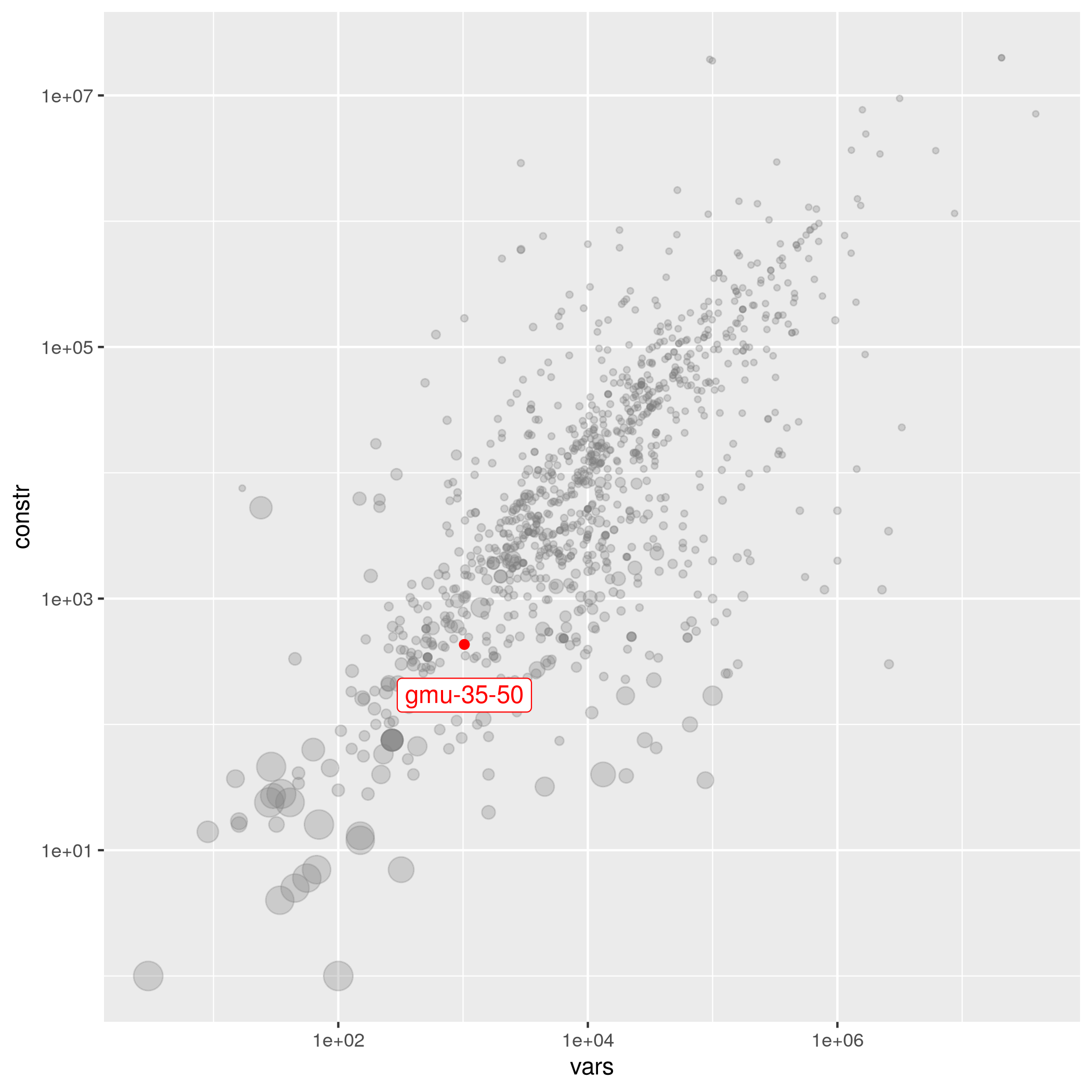
gmu-35-50

benchmark benchmark_suitable variable_bound set_packing mixed_binary

Submitter	Variables	Constraints	Density	Status	Group	Objective	MPS File
Nora Konnyu	1919	435	1.03538e-02	easy	gmu	-2607958.33	gmu-35-50.mps.gz

Timber harvest scheduling model These are harvest scheduling models of hypothetical forest planning problems where net timber revenues are maximized over a planning horizon subject to four sets of constraints: 1. Each management unit can be harvested only once over the planning horizon, 2. Volume harvested in one planning period should not be less or more than some portion of that in the preceding period, 3. Area-weighted average age of the forest by the end of the plan should notbe less than a certain target age. 4. Clearcut size in any planning period has to be below a specific limit. Decision variable are management units and generalized management units (group of management units with a combined area not exceeding the limit on clearcut size) and can be either fully harvested or left untouched in any planning period, therefore there is a binary restriction on the decision variables. Imported from the MIPLIB2010 submissions.

Location of instance in collection

Instance Statistics

Detailed explanation of the following tables can be found here.

Size Related Properties
	Original	Presolved
Variables	1919	1024
Constraints	435	432
Binaries	1914	1019
Integers	0	0
Continuous	5	5
Implicit Integers	0	0
Fixed Variables	0	0
Nonzero Density	0.0103538	0.0191854
Nonzeroes	8643	8487

Constraint Classification Properties
	Original	Presolved
Total	435	432
Empty	0	0
Free	0	0
Singleton	0	0
Aggregations	0	0
Precedence	0	0
Variable Bound	16	16
Set Partitioning	0	0
Set Packing	406	403
Set Covering	0	0
Cardinality	0	0
Invariant Knapsack	0	0
Equation Knapsack	0	0
Bin Packing	0	0
Knapsack	0	0
Integer Knapsack	0	0
Mixed Binary	13	13
General Linear	0	0
Indicator	0	0

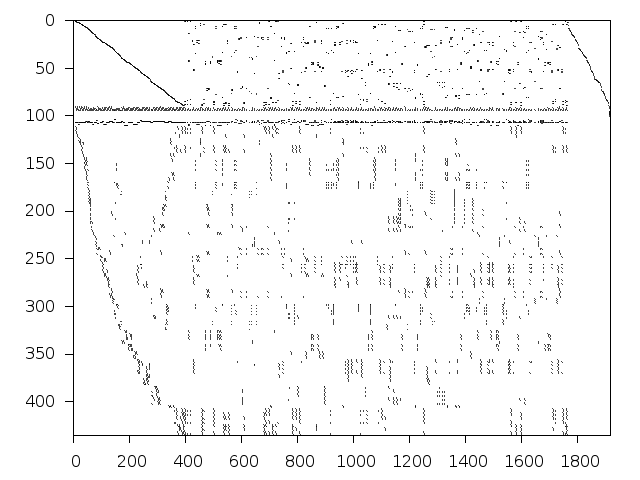
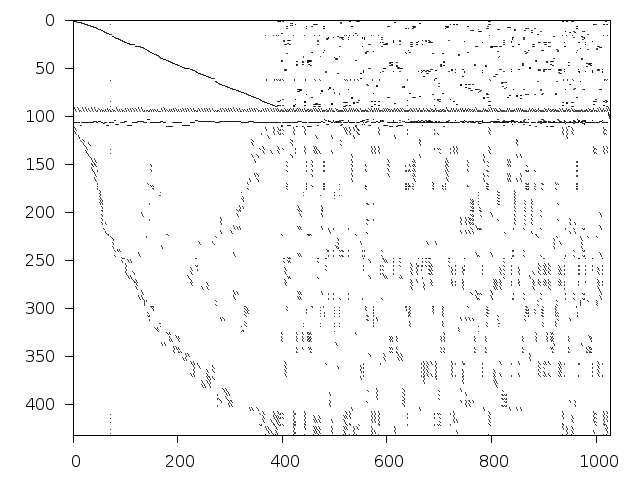
Structure

Available nonzero structure and decomposition information. Further information can be found here.

Nonzero entries of original problem

Nonzero entries after trivial presolving

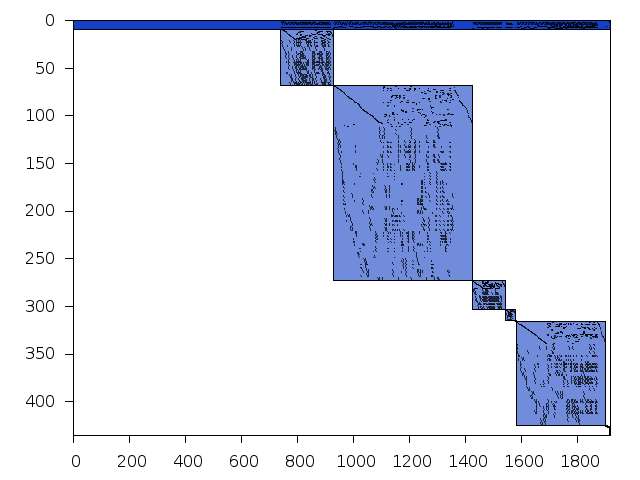
Decomposed structure of original problem (dec-file)

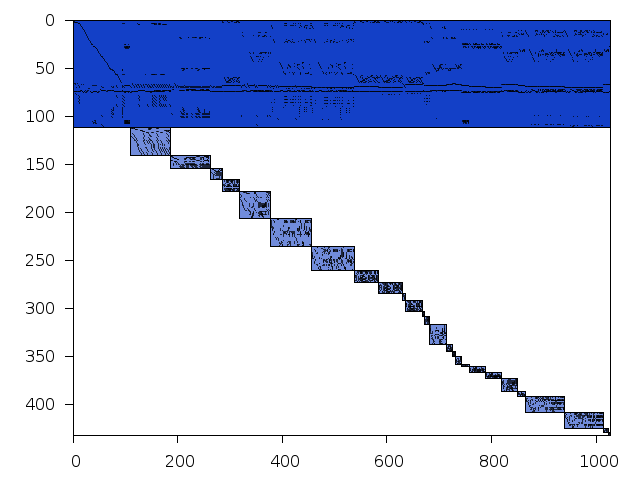
Decomposed structure after trivial presolving (dec-file)

	value	min	median	mean	max
Components	0.845098
Constraint %		1.851850	16.1651	10.1852	46.7593
Variable %		0.486855	16.6180	13.6806	41.6748
Score	0.673548

Best Known Solution(s)

Find solutions below. Download the archive containing all solutions from the Download page.

ID	Objective	Exact	Int. Viol	Cons. Viol	Obj. Viol	Submitter	Date	Description
2	-2607958	-2607958	0	0	0	-	2018-10-29	Solution found during MIPLIB2017 problem selection.
1	-2607958	-2607958	0	0	0	-	2018-10-12	Solution imported from MIPLIB2010.

Similar instances in collection

The following instances are most similar to gmu-35-50 in the collection. This similarity analysis is based on 100 scaled instance features describing properties of the variables, objective function, bounds, constraints, and right hand sides.

Instance	Status	Variables	Binaries	Continuous	Constraints	Nonz.	Submitter	Group	Objective	Tags
gmu-35-40	easy	1205	1200	5	424	4843	Nora Konnyu	gmu	-2406733.3688	benchmark benchmark_suitable variable_bound set_packing mixed_binary
gmut-76-40	open	24338	24332	6	2586	153017	Nora Konnyu	gmu	-14169477.79550346*	variable_bound set_packing mixed_binary
cap6000	easy	6000	6000	0	2176	48243	MIPLIB submission pool	–	-2451377	binary decomposition aggregations precedence variable_bound set_partitioning set_packing knapsack
gmut-76-50	open	68865	68859	6	2586	470045	Nora Konnyu	gmu	-14171893.7789212*	variable_bound set_packing mixed_binary
gmut-75-50	hard	68865	68859	6	2565	571475	Nora Konnyu	gmu	-14180699.047	variable_bound set_packing mixed_binary

Reference

No bibliographic information available