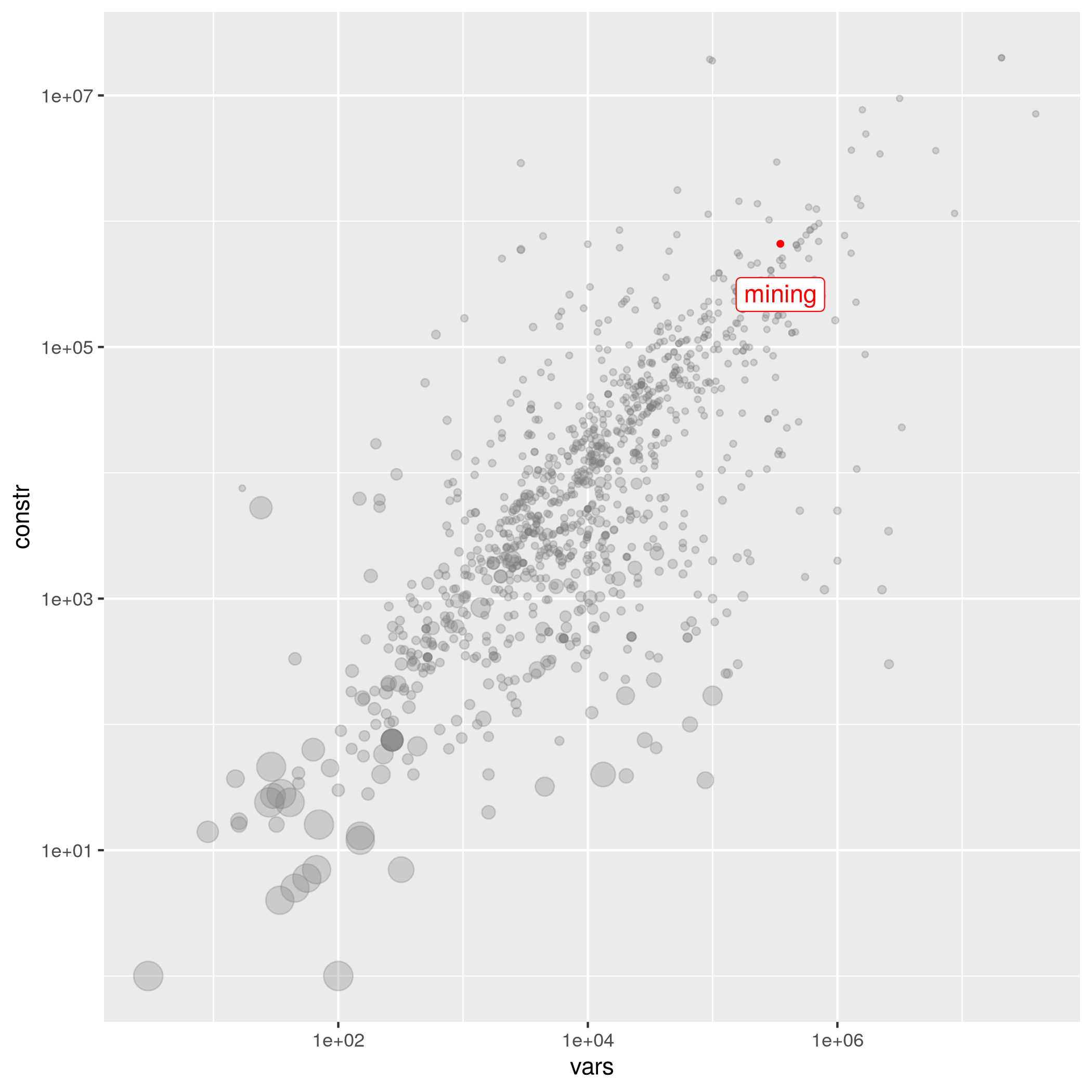
mining

binary numerics precedence invariant_knapsack mixed_binary

Submitter	Variables	Constraints	Density	Status	Group	Objective	MPS File
Kelly Eurek	348921	661133	1.66674e-05	open	–	-833555203.4089005*	mining.mps.gz

Unspecified mining application. Mark Zuckerberg suggests the following tightening of one class of constraints: The variables in this problem (except for the last one, x348921, which is fixed to 1 and does not appear in any constraint) are arranged in groups of 20, and there are three classes of precedence constraints (or more accurately, implication constraints): 1) For each variable index i=…,348920, if i mod 20 > 0 then there is a constraint x_i 2) If i mod 20 = and i>20 then there is a constraint x_i = x21 >= x41 >=…) 3) and for all other i there is a constraint x_i Graphically, we can represent the variables as a table with height twenty and width 348920 / 20, with indices 1,…,20 going down the left-most column, then 21,…,40 going down the next column to the right, etc. There is then a precedence constraint (1) from each variable in a column to the one below it, a precedence constraint (2) from the topmost entry in each column to its neighbor on the left, and an “OR” precedence constraint (3) from each entry that isn’t on top of a column, requiring that if it has value 1 then either the one above it or the one to its left must have value 1 as well. But in fact this OR precedence (3) can be replaced with a simple precedence constraint from each variable to the one at its left. To see this note that in any column, the first type of precedence constraint will require that a feasible solution must be a contiguous sequence of 1’s from some point in the column until the bottom. Consider column c > 1. The topmost 1 in this column, by precedence constraints (3) (or if the topmost is at the top of the column, then by precedence constraints (2)) implies that the variable to its left (in column c-1) is also 1, which implies that the contiguous sequence of 1’s in column c-1 must be at least as high as the sequence in column c. Thus for every 1 in column c, the entry to its left in column c-1 must also be 1. Imported from MIPLIB2010.

Location of instance in collection

Instance Statistics

Detailed explanation of the following tables can be found here.

Size Related Properties
	Original	Presolved
Variables	348921	348920
Constraints	661133	661132
Binaries	348920	348920
Integers	0	0
Continuous	1	0
Implicit Integers	0	0
Fixed Variables	0	0
Nonzero Density	1.66674e-05	1.66674e-05
Nonzeroes	3844880	3844880

Constraint Classification Properties
	Original	Presolved
Total	661133	661132
Empty	0	0
Free	0	0
Singleton	1	0
Aggregations	0	0
Precedence	347953	347953
Variable Bound	0	0
Set Partitioning	0	0
Set Packing	0	0
Set Covering	0	0
Cardinality	0	0
Invariant Knapsack	313101	313101
Equation Knapsack	0	0
Bin Packing	0	0
Knapsack	0	0
Integer Knapsack	0	0
Mixed Binary	78	78
General Linear	0	0
Indicator	0	0

Structure

Available nonzero structure and decomposition information. Further information can be found here.

Nonzero entries of original problem

Nonzero entries after trivial presolving

Decomposed structure of original problem (dec-file)

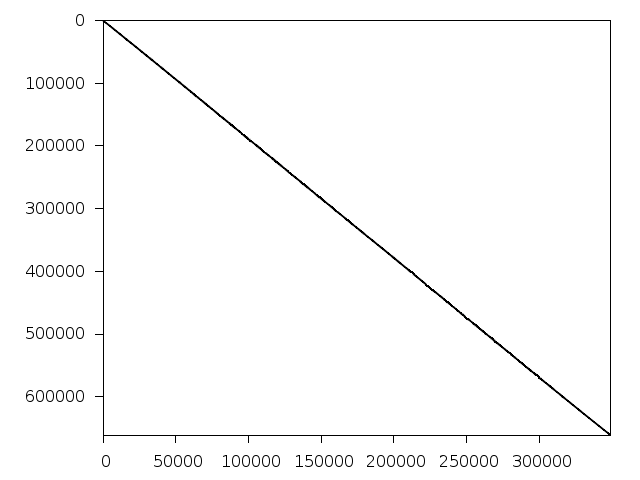
Decomposed structure after trivial presolving (dec-file)

	value	min	median	mean	max
Components
Constraint %
Variable %
Score

Best Known Solution(s)

Find solutions below. Download the archive containing all solutions from the Download page.

## Warning in lapply(df["exactobjval"], as.numeric): NAs introduced by coercion

ID	Objective	Exact	Obj. Viol	Submitter	Date	Description
3	-833555203	-833555203	4.0e-07	Edward Rothberg	2020-07-17	Obtained with the Gurobi 9.0 solution improvement heuristic
2	-797686257		5.0e-07	Robert Ashford and Alkis Vazacopoulus	2019-12-18	Found using ODH\|CPlex
1	531134255	531134255	2.7e-06	-	2018-10-12	Solution found during MIPLIB2017 problem selection.

Similar instances in collection

The following instances are most similar to mining in the collection. This similarity analysis is based on 100 scaled instance features describing properties of the variables, objective function, bounds, constraints, and right hand sides.

Instance	Status	Variables	Binaries	Constraints	Nonz.	Submitter	Group	Objective	Tags
rmine21	open	162547	162547	1441651	3514884	Daniel Espinoza	rmine	-10618.75083837232*	binary precedence mixed_binary
rmine25	open	326599	326599	2953849	7182744	Daniel Espinoza	rmine	-15541.66928749976*	binary precedence mixed_binary
rmine15	open	42438	42438	358395	879732	Daniel Espinoza	rmine	-5018.819990999996*	binary precedence mixed_binary
rmine13	open	23980	23980	197155	485784	Daniel Espinoza	rmine	-3495.3706624382535*	binary precedence mixed_binary
opm2-z12-s8	hard	10800	10800	319508	725377	Daniel Espinoza	opm2	-58540	binary precedence knapsack

Reference

No bibliographic information available