stp3d

binary decomposition aggregations precedence variable_bound set_partitioning set_packing cardinality

Submitter	Variables	Constraints	Density	Status	Group	Objective	MPS File
T. Koch	204880	159488	2.02635e-05	hard	–	493.71965	stp3d.mps.gz

Steiner tree packing instance in a 3 dimensional grid-graph, LP relaxation is highly degenerate. Alkis Vazacopoulos reports finding the first feasible solution of this instance using XPRESS 2006B. This instance was solved by a first implementation of ParaSCIP using up to 2048 cores of HLRN-II(https://www.hlrn.de). ParaSCIP, mainly developed by Yuji Shinano, is an extension of SCIP and realizes a parallelization on a distributed memory computing environment. For being able to interrupt and warmstart the computations, ParaSCIP has a checkpoint mechanism. Therefore, selected subproblems are stored as warm start information, which allows to virtually run ParaSCIP, although the HLRN-II environment imposes a time limit of 48 hours per run. The problem was presolved several times with SCIP presolving techniques. After that, it took approximately 114 hours to solve this instance. Imported from MIPLIB2010.

Location of instance in collection

Instance Statistics

Detailed explanation of the following tables can be found here.

Size Related Properties
	Original	Presolved
Variables	204880	179062
Constraints	159488	139386
Binaries	204880	179062
Integers	0	0
Continuous	0	0
Implicit Integers	0	0
Fixed Variables	0	0
Nonzero Density	2.02635e-05	2.33948e-05
Nonzeroes	662128	583904

Constraint Classification Properties
	Original	Presolved
Total	159488	139386
Empty	0	0
Free	0	0
Singleton	0	0
Aggregations	0	94
Precedence	129232	112973
Variable Bound	0	50
Set Partitioning	82	23
Set Packing	2171	1965
Set Covering	0	0
Cardinality	28003	24281
Invariant Knapsack	0	0
Equation Knapsack	0	0
Bin Packing	0	0
Knapsack	0	0
Integer Knapsack	0	0
Mixed Binary	0	0
General Linear	0	0
Indicator	0	0

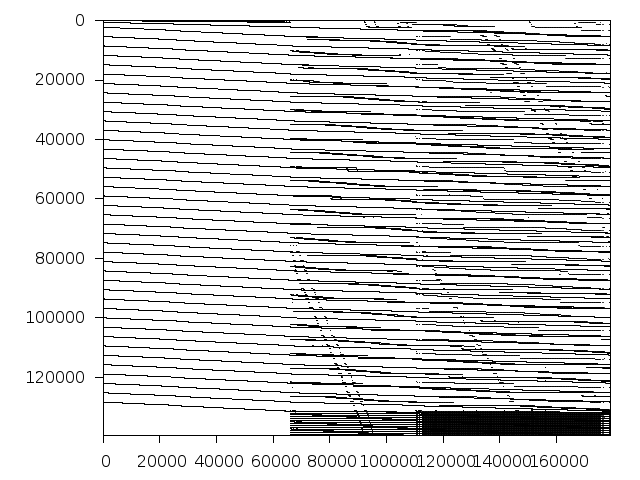
Structure

Available nonzero structure and decomposition information. Further information can be found here.

Nonzero entries of original problem

Nonzero entries after trivial presolving

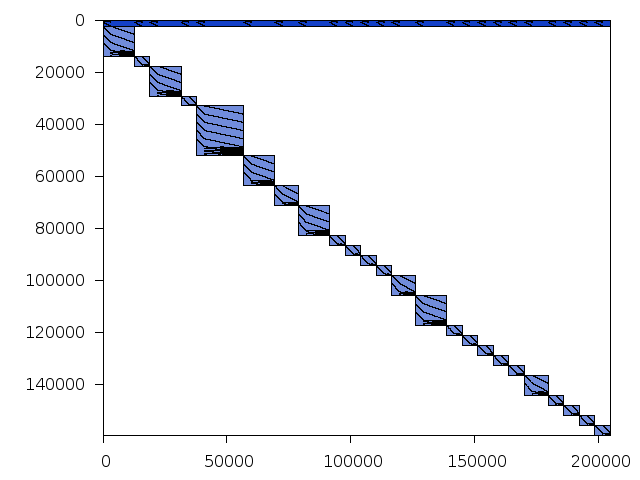
Decomposed structure of original problem (dec-file)

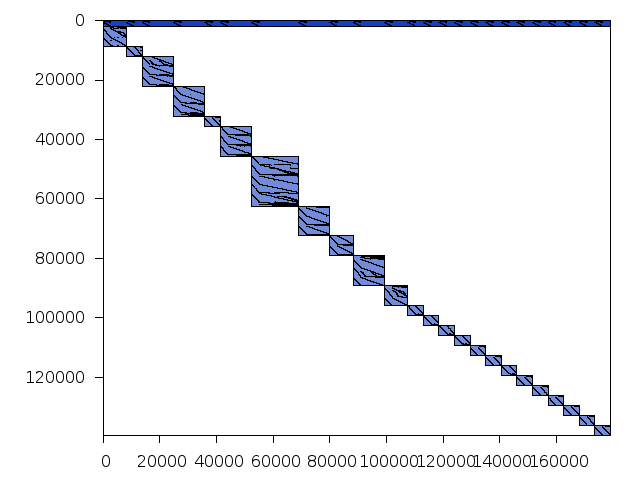
Decomposed structure after trivial presolving (dec-file)

	value	min	median	mean	max
Components	1.672098
Constraint %		0.00215	2.14327	2.39622	12.05640
Variable %		0.00223	2.17372	3.06850	9.25909
Score	0.934837

Best Known Solution(s)

No solution available for stp3d .

Similar instances in collection

The following instances are most similar to stp3d in the collection. This similarity analysis is based on 100 scaled instance features describing properties of the variables, objective function, bounds, constraints, and right hand sides.

Instance	Status	Variables	Binaries	Continuous	Constraints	Nonz.	Submitter	Group	Objective	Tags
neos-631710	easy	167056	167056	0	169576	834166	NEOS Server Submission	neos-pseudoapplication-75	203	benchmark binary benchmark_suitable precedence set_partitioning set_packing binpacking
ns1828997	open	27275	27275	0	81725	190670	NEOS Server Submission	neos-pseudoapplication-13	7.99999999999967*	binary precedence variable_bound cardinality invariant_knapsack
neos-4295773-pissa	hard	85126	85124	2	210116	552408	Jeff Linderoth	neos-pseudoapplication-6	0.03830719099856019	decomposition aggregations precedence variable_bound set_partitioning cardinality invariant_knapsack knapsack mixed_binary
neos-4300652-rahue	easy	33003	20900	12103	76992	183616	Jeff Linderoth	neos-pseudoapplication-13	2.1416	benchmark decomposition benchmark_suitable aggregations precedence variable_bound set_partitioning cardinality knapsack mixed_binary
supportcase29	easy	12050	12050	0	12441	96050	Domenico Salvagnin	–	Infeasible	infeasible binary decomposition benchmark_suitable precedence set_packing invariant_knapsack binpacking knapsack mixed_binary

Reference

@phdthesis{Koch2004,
 author = {Thorsten Koch},
 language = {English},
 school = {Technische {Universit\"at} Berlin},
 title = {Rapid Mathematical Programming},
 year = {2004}
}