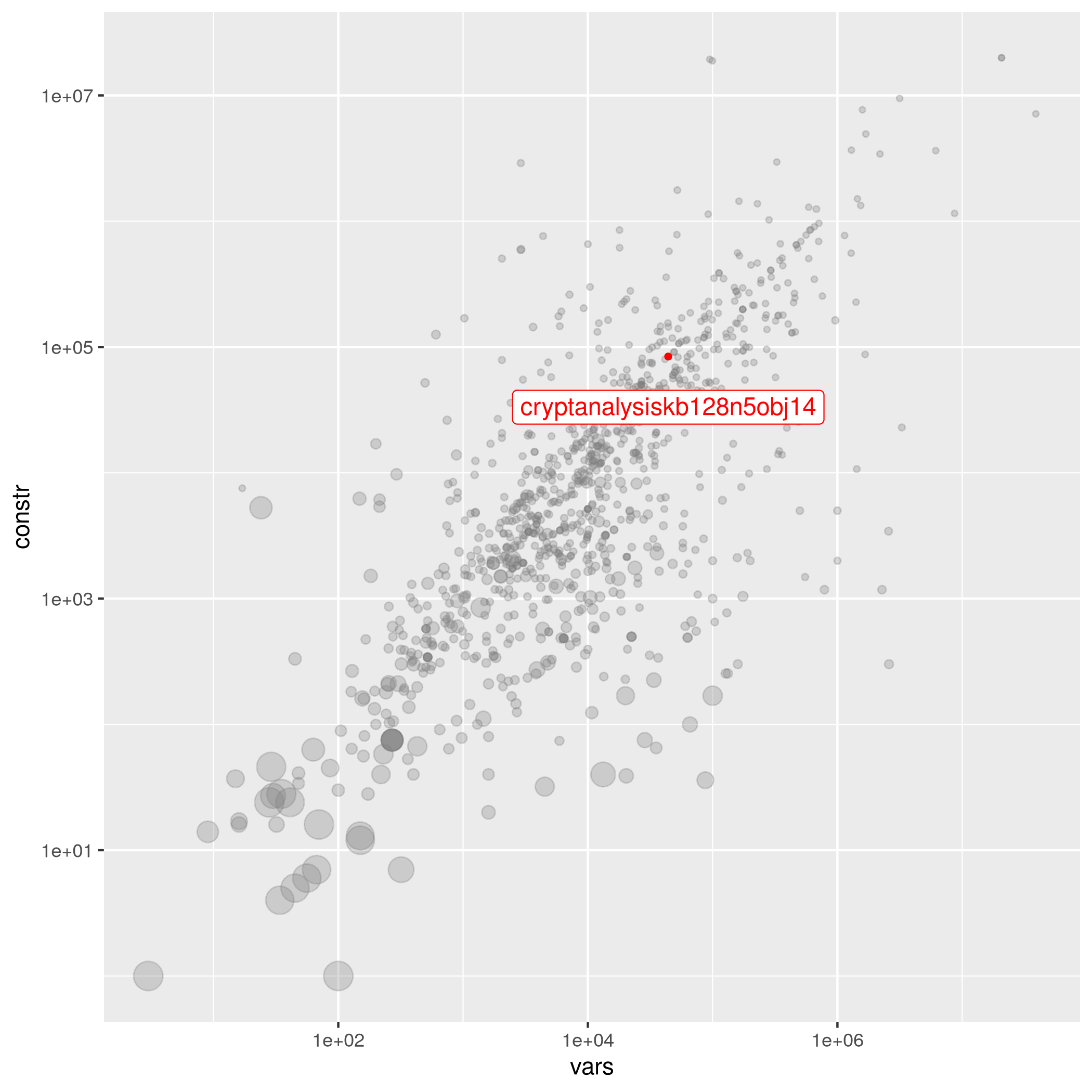
cryptanalysiskb128n5obj14

benchmark infeasible feasibility benchmark_suitable aggregations precedence variable_bound set_covering cardinality invariant_knapsack binpacking knapsack integer_knapsack mixed_binary general_linear

Submitter	Variables	Constraints	Density	Status	Group	Objective	MPS File
Gleb Belov	48950	98021	6.10394e-05	hard	cryptanalysis	Infeasible	cryptanalysiskb128n5obj14.mps.gz

Linearized Constraint Programming models of the MiniZinc Challenges 2012-2016. I should be able to produce versions with indicator constraints supported by Gurobi and CPLEX, however don’t know if you can use them and if there is a standard format. These MPS were produced by Gurobi 7.0.2 using the MiniZinc develop branch on eb536656062ca13325a96b5d0881742c7d0e3c38

Location of instance in collection

Instance Statistics

Detailed explanation of the following tables can be found here.

Size Related Properties
	Original	Presolved
Variables	48950	44076
Constraints	98021	84009
Binaries	47830	42956
Integers	1120	1120
Continuous	0	0
Implicit Integers	0	0
Fixed Variables	1328	0
Nonzero Density	6.10394e-05	6.85450e-05
Nonzeroes	292875	253807

Constraint Classification Properties
	Original	Presolved
Total	98022	84010
Empty	0	0
Free	0	0
Singleton	0	0
Aggregations	4668	7278
Precedence	20258	11950
Variable Bound	11124	11878
Set Partitioning	0	0
Set Packing	0	0
Set Covering	0	2422
Cardinality	6116	3482
Invariant Knapsack	12770	9856
Equation Knapsack	0	0
Bin Packing	25098	2946
Knapsack	17910	13176
Integer Knapsack	1	1
Mixed Binary	0	20944
General Linear	77	77
Indicator	0	0

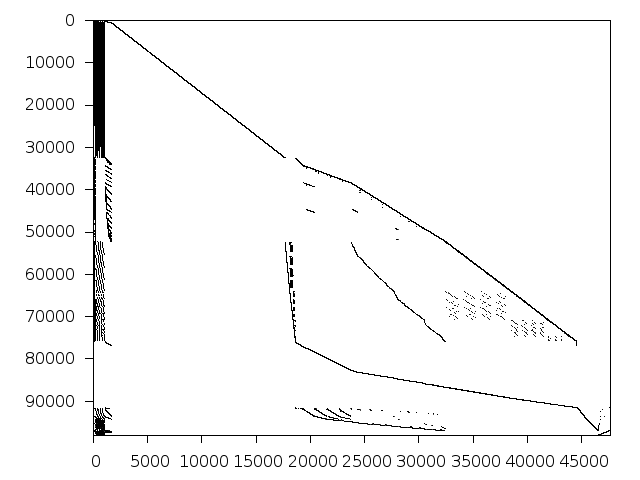
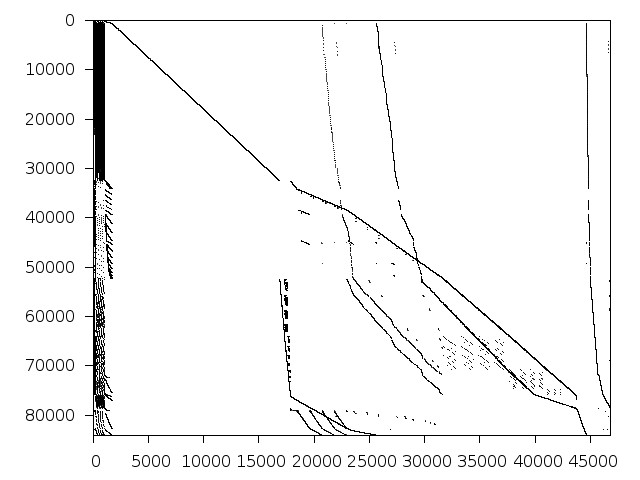
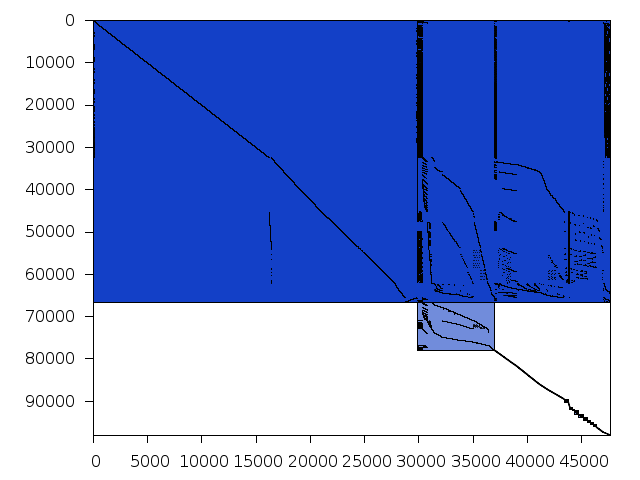
Structure

Available nonzero structure and decomposition information. Further information can be found here.

Nonzero entries of original problem

Nonzero entries after trivial presolving

Decomposed structure of original problem (dec-file)

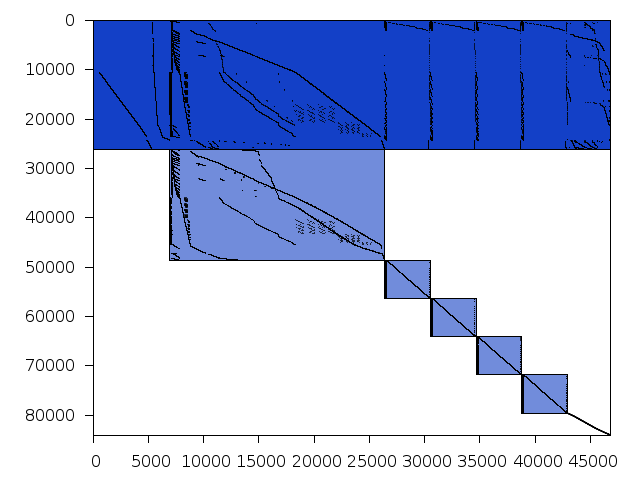
Decomposed structure after trivial presolving (dec-file)

	value	min	median	mean	max
Components	2.970812
Constraint %		0.00238	0.0738526	0.00357	26.8162
Variable %		0.00427	0.0912005	0.00641	41.5368
Score	0.545821

Best Known Solution(s)

No solution available for cryptanalysiskb128n5obj14 .

Similar instances in collection

The following instances are most similar to cryptanalysiskb128n5obj14 in the collection. This similarity analysis is based on 100 scaled instance features describing properties of the variables, objective function, bounds, constraints, and right hand sides.

Instance	Status	Variables	Binaries	Integers	Continuous	Constraints	Nonz.	Submitter	Group	Objective	Tags
cryptanalysiskb128n5obj16	easy	48950	47830	1120	0	98021	292875	Gleb Belov	cryptanalysis	0	benchmark feasibility benchmark_suitable aggregations precedence variable_bound set_covering cardinality invariant_knapsack binpacking knapsack integer_knapsack mixed_binary general_linear
gfd-schedulen180f7d50m30k18	easy	227535	192408	2025	33102	457985	1233372	Gleb Belov	gfd-schedule	1	benchmark feasibility benchmark_suitable aggregations precedence variable_bound set_partitioning cardinality invariant_knapsack mixed_binary general_linear
fhnw-binpack4-58	open	7550	7400	0	150	9900	35750	Simon Felix	binpack		no_solution feasibility precedence variable_bound invariant_knapsack mixed_binary
neos-3603137-hoteo	open	4003	3913	90	0	10510	39146	Jeff Linderoth	neos-pseudoapplication-38		no_solution feasibility aggregations set_covering invariant_knapsack knapsack general_linear
supportcase4	easy	3162	3162	0	0	9492	38036	Michael Winkler	–	0	binary feasibility benchmark_suitable aggregations precedence variable_bound invariant_knapsack knapsack mixed_binary

Reference

@Inbook{Belov2016,
author="Belov, Gleb
and Stuckey, Peter J.
and Tack, Guido
and Wallace, Mark",
editor="Rueher, Michel",
title="Improved Linearization of Constraint Programming Models",
bookTitle="Principles and Practice of Constraint Programming: 22nd International Conference, CP 2016, Toulouse, France, September 5-9, 2016, Proceedings",
year="2016",
publisher="Springer International Publishing",
pages="49--65",
isbn="978-3-319-44953-1",
doi="10.1007/978-3-319-44953-1_4",
url="http://dx.doi.org/10.1007/978-3-319-44953-1_4"
}