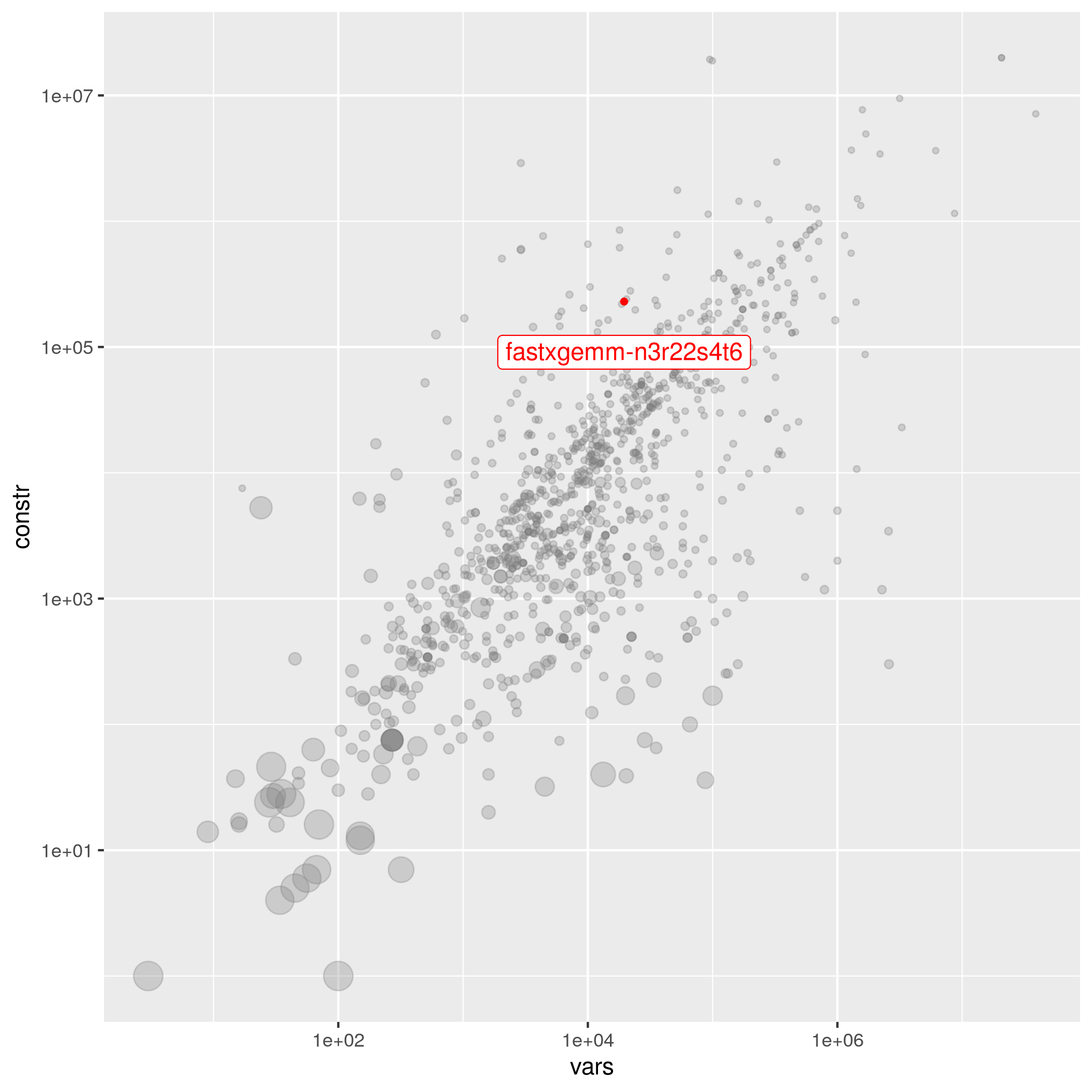
fastxgemm-n3r22s4t6

decomposition variable_bound set_partitioning set_covering mixed_binary general_linear

Submitter	Variables	Constraints	Density	Status	Group	Objective	MPS File
Laurent Sorber	19539	229742	1.67584e-04	open	fastxgemm	3101.998198399999*	fastxgemm-n3r22s4t6.mps.gz

Naive multiplication of two N by N matrices requires N^3 scalar multiplications. For N=2, Strassen showed that it could be done in only R=7 < 8=N^3 multiplications. For N=3, it is known that 19 <= R <= 23, and for N=4 it is known that 34 <= R <= 49. This repository contains code that generates a mixed-integer linear program (MILP) formulation of the fast matrix multiplication problem for finding solutions with R < N^3 and proving that they are optimal. For a more detailed description, see the accompanying manuscript.

Location of instance in collection

Instance Statistics

Detailed explanation of the following tables can be found here.

Size Related Properties
	Original	Presolved
Variables	19539	19539
Constraints	229742	229742
Binaries	396	396
Integers	0	1188
Continuous	19143	17955
Implicit Integers	0	1188
Fixed Variables	0	0
Nonzero Density	0.000167584	0.000167584
Nonzeroes	752274	752274

Constraint Classification Properties
	Original	Presolved
Total	229742	229742
Empty	0	0
Free	0	0
Singleton	0	0
Aggregations	0	0
Precedence	48708	0
Variable Bound	48708	97416
Set Partitioning	0	594
Set Packing	0	0
Set Covering	0	93
Cardinality	0	0
Invariant Knapsack	0	0
Equation Knapsack	0	0
Bin Packing	0	0
Knapsack	0	0
Integer Knapsack	0	0
Mixed Binary	132326	2741
General Linear	0	128898
Indicator	0	0

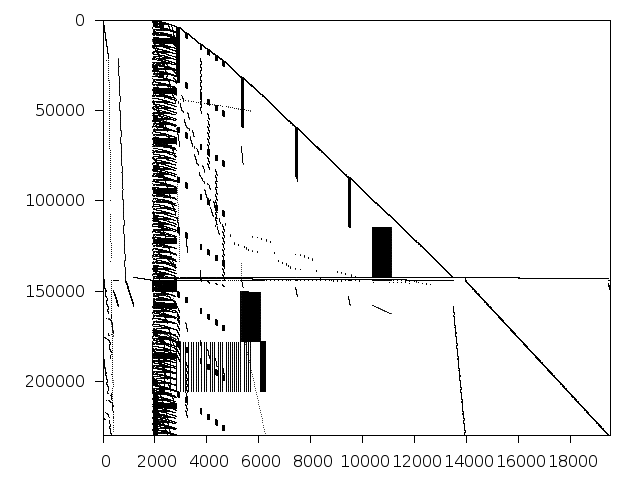
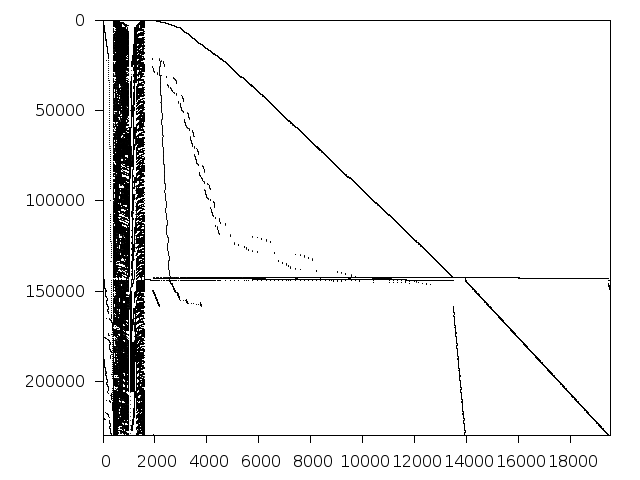
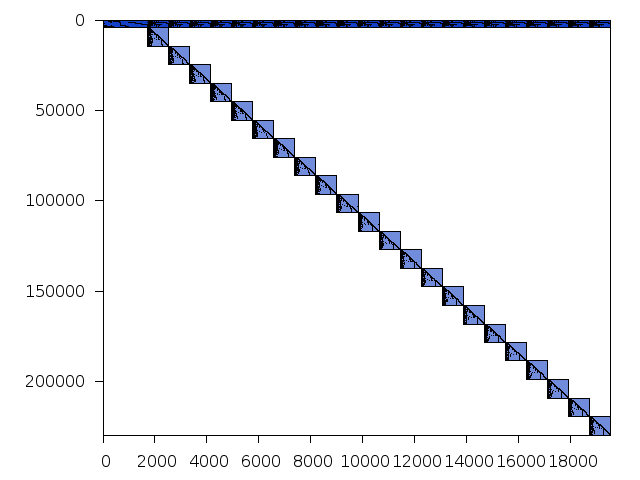
Structure

Available nonzero structure and decomposition information. Further information can be found here.

Nonzero entries of original problem

Nonzero entries after trivial presolving

Decomposed structure of original problem (dec-file)

Decomposed structure after trivial presolving (dec-file)

	value	min	median	mean	max
Components	1.361728
Constraint %		4.46588	4.46588	4.46588	4.46588
Variable %		4.14556	4.14556	4.14556	4.14556
Score	0.941764

Best Known Solution(s)

Find solutions below. Download the archive containing all solutions from the Download page.

## Warning in lapply(df["exactobjval"], as.numeric): NAs introduced by coercion

ID	Objective	Exact	Cons. Viol	Submitter	Date	Description
5	3101.998	3102	5e-07	Alex Fender, Alice Boucher, Akif Coerduek, Piotr Sielski, Burcin Bozkaya, Preethi Maulik	2025-01-10	Found using GPU-accelerated MIP in NVIDIA cuOpt
4	3101.998		5e-07	Edward Rothberg	2019-12-13	Obtained with Gurobi 9.0
3	6084.000	6084	0e+00	Frederic Didier	2020-01-22	Obtained with Google OR-tools using 8 Threads through generating subproblems by fixing part of the current solution and trying to solve them with a sub CP-SAT solver
2	6087.000		0e+00	Robert Ashford and Alkis Vazacopoulos	2019-12-18	Found using ODH\|CPlex
1	21084.000	21084	0e+00	-	2018-10-13	Solution found during MIPLIB2017 problem selection.

Similar instances in collection

The following instances are most similar to fastxgemm-n3r22s4t6 in the collection. This similarity analysis is based on 100 scaled instance features describing properties of the variables, objective function, bounds, constraints, and right hand sides.

Instance	Status	Variables	Binaries	Integers	Continuous	Constraints	Nonz.	Submitter	Group	Objective	Tags
fastxgemm-n3r23s5t6	open	20394	414	0	19980	240116	786402	Laurent Sorber	fastxgemm	3089.997998*	decomposition variable_bound set_partitioning set_covering mixed_binary general_linear
fastxgemm-n3r21s3t6	open	18684	378	0	18306	219368	718146	Laurent Sorber	fastxgemm	4110.99800117485*	decomposition variable_bound set_partitioning set_covering mixed_binary general_linear
fastxgemm-n2r7s4t1	easy	904	56	0	848	6972	22584	Laurent Sorber	fastxgemm	41.99999999999998	decomposition benchmark_suitable variable_bound set_partitioning set_covering mixed_binary general_linear
fastxgemm-n2r6s0t2	easy	784	48	0	736	5998	19376	Laurent Sorber	fastxgemm	230	benchmark decomposition benchmark_suitable variable_bound set_partitioning set_covering mixed_binary general_linear
neos-4335793-snake	hard	30827	20473	7865	2489	37166	129119	Jeff Linderoth	neos-pseudoapplication-44	27	numerics aggregations precedence variable_bound set_packing cardinality invariant_knapsack knapsack mixed_binary general_linear

Reference

@misc{Sorber2017,
author = {Laurent Sorber and Marc Van Barel},
title = {{A mixed-integer linear program formulation for fast matrix multiplication}},
howpublished = "\url{https://github.com/lsorber/fast-matrix-multiplication/blob/master/latex/fast-matrix-multiplication.pdf}",
day = {30},
month = {April},
year = {2017}, 
note = "[Online]"
}