highschool1-aigio

benchmark benchmark_suitable aggregations variable_bound set_partitioning set_packing set_covering cardinality invariant_knapsack equation_knapsack general_linear

Submitter	Variables	Constraints	Density	Status	Group	Objective	MPS File
George Fonseca	320404	92568	5.26707e-05	hard	timetabling	0	highschool1-aigio.mps.gz

Educational timetabling problems from several real schools/universities around the world. These instances were originally expressed in the xhstt file format [1] and formulated as Integer Programming models as described at [2].

[1] https://www.sciencedirect.com/science/article/pii/S0377221717302242 [2] https://link.springer.com/article/10.1007/s10479-011-1012-2

Location of instance in collection

Instance Statistics

Detailed explanation of the following tables can be found here.

Size Related Properties
	Original	Presolved
Variables	320404	305241
Constraints	92568	85087
Binaries	319686	304523
Integers	718	718
Continuous	0	0
Implicit Integers	0	190
Fixed Variables	0	0
Nonzero Density	5.26707e-05	5.66134e-05
Nonzeroes	1562170	1470370

Constraint Classification Properties
	Original	Presolved
Total	92568	85087
Empty	283	0
Free	0	0
Singleton	294	0
Aggregations	5840	5221
Precedence	0	0
Variable Bound	19870	17360
Set Partitioning	17329	18317
Set Packing	9291	9230
Set Covering	532	1512
Cardinality	9153	6890
Invariant Knapsack	10094	7518
Equation Knapsack	18620	17962
Bin Packing	0	0
Knapsack	0	0
Integer Knapsack	0	0
Mixed Binary	0	0
General Linear	1262	1077
Indicator	0	0

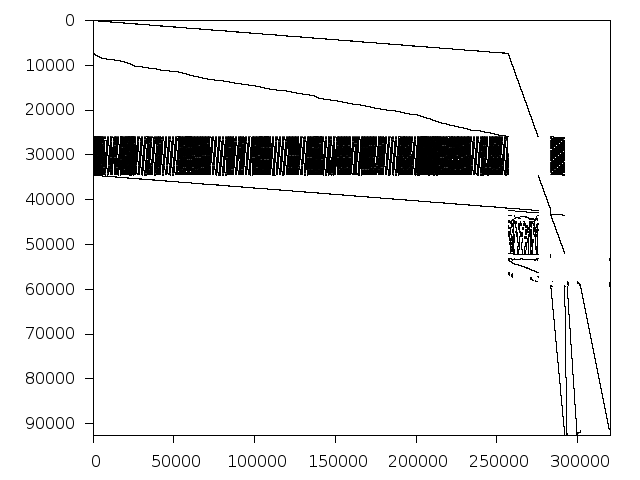
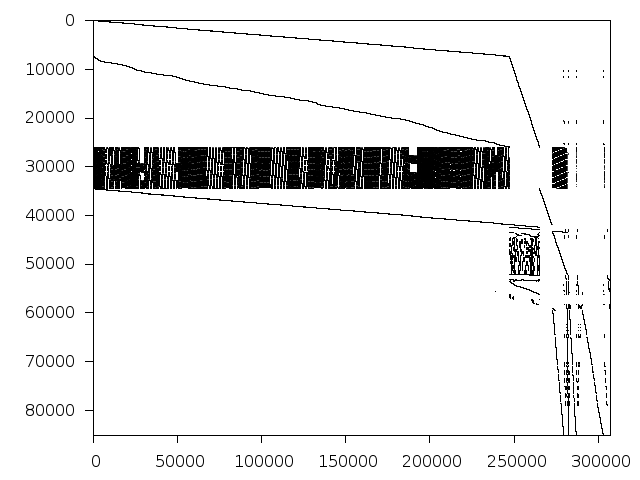
Structure

Available nonzero structure and decomposition information. Further information can be found here.

Nonzero entries of original problem

Nonzero entries after trivial presolving

Decomposed structure of original problem (dec-file)

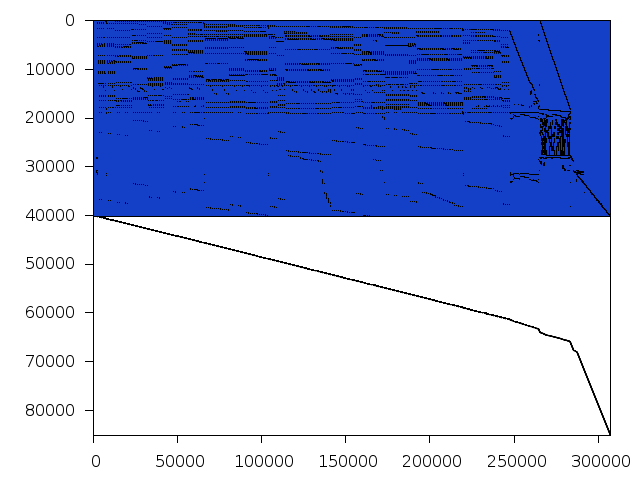
Decomposed structure after trivial presolving (dec-file)

	value	min	median	mean	max
Components
Constraint %
Variable %
Score

Best Known Solution(s)

No solution available for highschool1-aigio .

Similar instances in collection

The following instances are most similar to highschool1-aigio in the collection. This similarity analysis is based on 100 scaled instance features describing properties of the variables, objective function, bounds, constraints, and right hand sides.

Instance	Status	Variables	Binaries	Integers	Continuous	Constraints	Nonz.	Submitter	Group	Objective	Tags
triptim2	hard	27326	20776	6543	7	14427	521898	MIPLIB submission pool	triptim	12.0051	aggregations precedence variable_bound set_partitioning set_packing set_covering cardinality invariant_knapsack general_linear
triptim4	hard	27226	18537	8682	7	14361	520532	MIPLIB submission pool	triptim	9.818099999800323	aggregations precedence variable_bound set_partitioning set_packing set_covering invariant_knapsack general_linear
triptim1	easy	30055	20456	9592	7	15706	515436	MIPLIB submission pool	triptim	22.8680999999999	benchmark benchmark_suitable aggregations precedence variable_bound set_partitioning set_packing set_covering invariant_knapsack general_linear
kottenpark09	open	2893026	2892333	693	0	325547	13085485	George Fonseca	timetabling	1715.0*	aggregations precedence variable_bound set_partitioning set_packing set_covering cardinality invariant_knapsack mixed_binary general_linear
kosova1	open	614253	609591	4662	0	304931	3414761	George Fonseca	timetabling	6.0*	aggregations precedence variable_bound set_partitioning set_packing set_covering cardinality invariant_knapsack equation_knapsack binpacking general_linear

Reference

@article{FONSECA201728,
title = "Integer programming techniques for educational timetabling",
journal = "European Journal of Operational Research",
volume = "262",
number = "1",
pages = "28 - 39",
year = "2017",
note = "",
issn = "0377-2217",
doi = "http://dx.doi.org/10.1016/j.ejor.2017.03.020",
url = "http://www.sciencedirect.com/science/article/pii/S0377221717302242",
author = "George H.G. Fonseca and Haroldo G. Santos and Eduardo G. Carrano and Thomas J.R. Stidsen",
keywords = "Timetabling",
keywords = "Integer Programming",
keywords = "Formulation"
}