kosova1
aggregations precedence variable_bound set_partitioning set_packing set_covering cardinality invariant_knapsack equation_knapsack binpacking general_linear
| Submitter | Variables | Constraints | Density | Status | Group | Objective | MPS File |
|---|---|---|---|---|---|---|---|
| George Fonseca | 614253 | 304931 | 1.8231e-05 | hard | timetabling | 0.0 | kosova1.mps.gz |
Educational timetabling problems from several real schools/universities around the world. These instances were originally expressed in the xhstt file format [1] and formulated as Integer Programming models as described at [2].
[1] https://doi.org/10.1016/j.ejor.2017.03.020 [2] https://doi.org/10.1007/s10479-011-1012-2
Location of instance in collection
Instance Statistics
Detailed explanation of the following tables can be found here.
| Original | Presolved | |
|---|---|---|
| Variables | 614253 | 333136 |
| Constraints | 304931 | 176993 |
| Binaries | 609591 | 328474 |
| Integers | 4662 | 4662 |
| Continuous | 0 | 0 |
| Implicit Integers | 0 | 4531 |
| Fixed Variables | 0 | 0 |
| Nonzero Density | 1.82310e-05 | 2.78912e-05 |
| Nonzeroes | 3414760 | 1644540 |
| Original | Presolved | |
|---|---|---|
| Total | 304931 | 176993 |
| Empty | 875 | 0 |
| Free | 0 | 0 |
| Singleton | 1053 | 0 |
| Aggregations | 2460 | 2761 |
| Precedence | 30504 | 18321 |
| Variable Bound | 26404 | 18598 |
| Set Partitioning | 21052 | 18774 |
| Set Packing | 8301 | 8301 |
| Set Covering | 2767 | 1491 |
| Cardinality | 11141 | 6735 |
| Invariant Knapsack | 13359 | 10019 |
| Equation Knapsack | 173040 | 82988 |
| Bin Packing | 0 | 41 |
| Knapsack | 126 | 0 |
| Integer Knapsack | 0 | 0 |
| Mixed Binary | 0 | 0 |
| General Linear | 13849 | 8964 |
| Indicator | 0 | 0 |
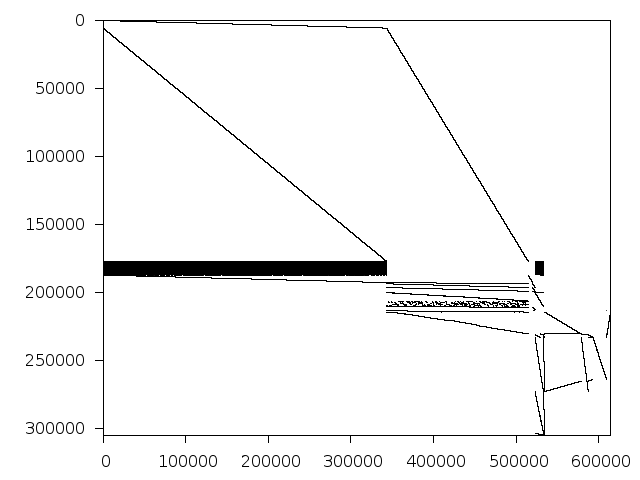
Structure
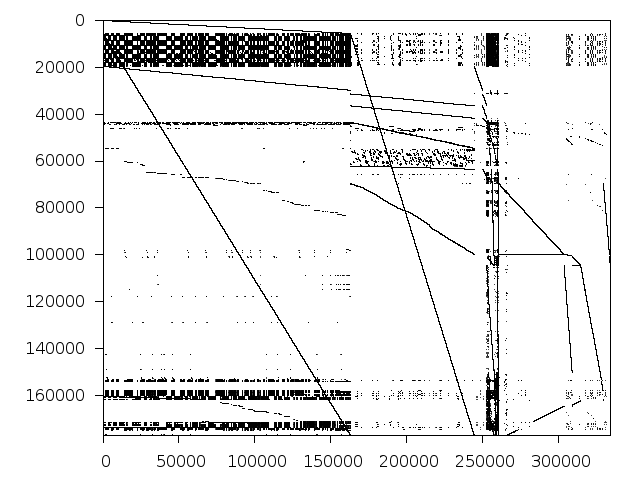
Available nonzero structure and decomposition information. Further information can be found here.
Nonzero entries of original problem
Nonzero entries after trivial presolving
Decomposed structure of original problem (dec-file)
Decomposed structure after trivial presolving (dec-file)
| value | min | median | mean | max | |
|---|---|---|---|---|---|
| Components | |||||
| Constraint % | |||||
| Variable % | |||||
| Score |
Best Known Solution(s)
Find solutions below. Download the archive containing all solutions from the Download page.
## Warning in lapply(df["exactobjval"], as.numeric): NAs introduced by coercion| ID | Objective | Exact | Int. Viol | Cons. Viol | Obj. Viol | Submitter | Date | Description |
|---|---|---|---|---|---|---|---|---|
| 5 | 0 | 0 | 0 | 0 | 0 | Jiongzhi Zheng | 2024-12-16 | OptVerse using 12 threads over two days |
| 4 | 6 | 6 | 0 | 0 | 0 | Mars Davletshin | 2023-12-12 | The initial solution was obtained using neural primal heuristic and then improved using solution improvement heuristic with Huawei OptVerse solver. |
| 3 | 293 | 293 | 0 | 0 | 0 | Edward Rothberg | 2020-11-25 | Found with Gurobi 9.1 NoRel heuristics |
| 2 | 357 | 357 | 0 | 0 | 0 | Edward Rothberg | 2020-09-14 | Found with Gurobi |
| 1 | 526 | 0 | 0 | 0 | Robert Ashford and Alkis Vazacopoulos | 2019-11-15 | Found by the Optimization Direct Heuristic and CPLEX |
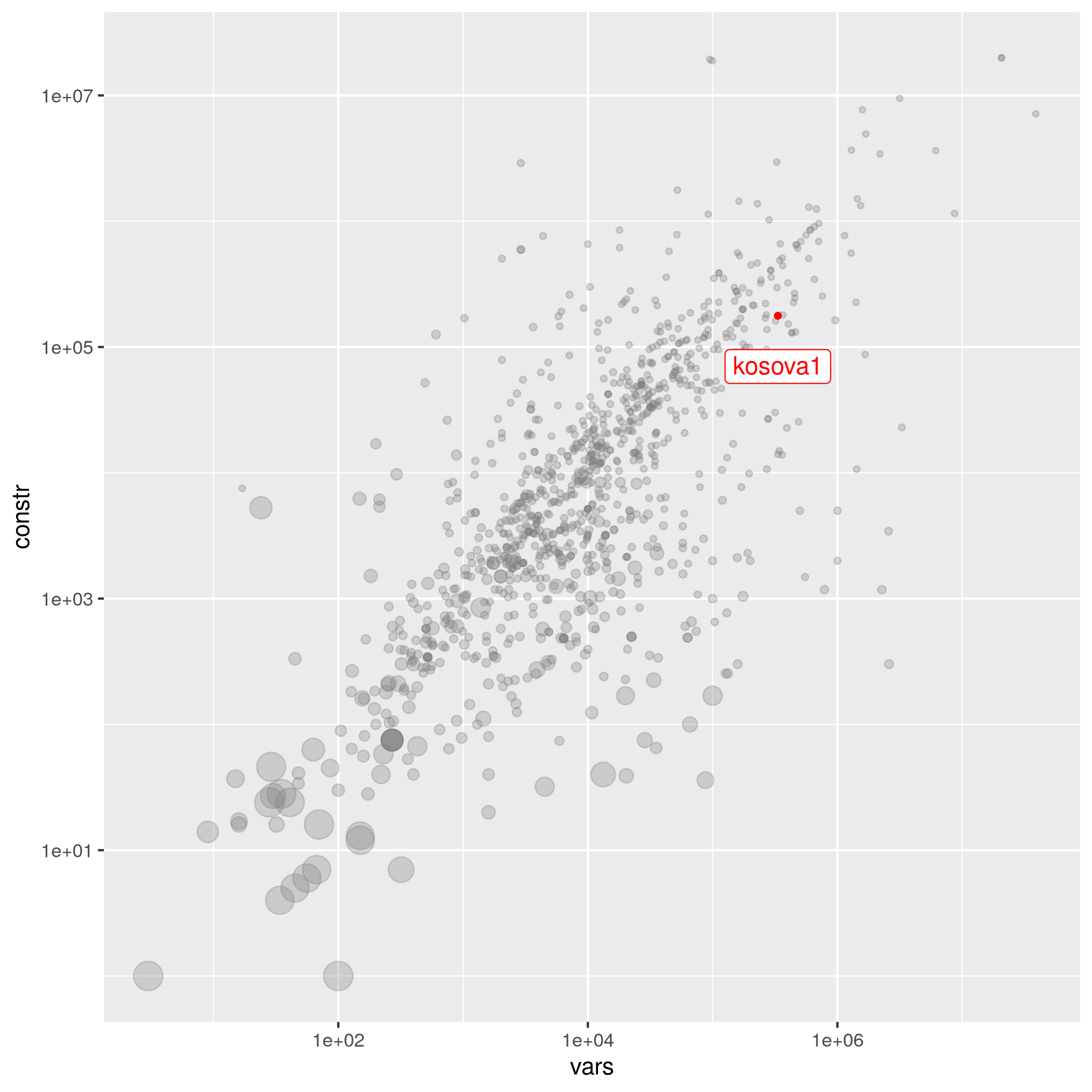
Similar instances in collection
The following instances are most similar to kosova1 in the collection. This similarity analysis is based on 100 scaled instance features describing properties of the variables, objective function, bounds, constraints, and right hand sides.
Reference
@article{FONSECA201728,
title = "Integer programming techniques for educational timetabling",
journal = "European Journal of Operational Research",
volume = "262",
number = "1",
pages = "28 - 39",
year = "2017",
note = "",
issn = "0377-2217",
doi = "http://dx.doi.org/10.1016/j.ejor.2017.03.020",
url = "http://www.sciencedirect.com/science/article/pii/S0377221717302242",
author = "George H.G. Fonseca and Haroldo G. Santos and Eduardo G. Carrano and Thomas J.R. Stidsen",
keywords = "Timetabling",
keywords = "Integer Programming",
keywords = "Formulation"
}Last Update 2025 by Mark Turner
generated with R Markdown
© by Zuse Institute Berlin (ZIB)
Imprint